他因七巧板而愛上數學謎題，如今破解一個百年難題
本文來自微信公眾號：返樸 （ID：fanpu2019），作者：嘉偉，題圖來自：視覺中國
似乎人類很喜歡拚圖類的遊戲。在不同的文明中，各式各樣的拚圖玩具被不同時代的人反復發明。根據著名的《阿基米德重寫本》（Archimedes Palimpsest），阿基米德曾將一個正方形分解成14塊，思考如何將碎片以不同的方式重新組合在一起，形成一個正方形。源自中國的七巧板，更是給世界各地的兒童帶來無限樂趣的益智玩具。今年5月末，一位兒時因七巧板愛上破解謎題、進而創造謎題的芬蘭人，解決了一個數學上的百年謎題。
阿基米德的14塊碎片拚正方形難題Ostomachion。丨圖源：Dissection puzzle – Wikipedia剖分謎題
在19世紀後期，當報紙和雜誌開始刊登各種智力趣題填充版面時，這些謎題的受歡迎程度大大提高。美國的益智謎題創作者薩姆·勞艾達馬田斯（Sam Loyd）和英國的亨利·杜德尼（Henry Dudeney）是最受歡迎的出題人。從那時起，拚圖和相關衍生謎題就被用於娛樂和數學教育。
勞艾達馬田斯曾向公眾發起智力挑戰：一個木匠需要將一個主教冠形狀（一個正方形切去1/4，即剔除一個等腰直角三角形後）的木板切割成幾塊（要求塊數最小），才能經過再拚接，重組成一個小正方形？勞艾達馬田斯後來給出了自己的答案，遺憾的是，他的構造並不正確。勞艾達馬田斯認為分成適當的4小塊，便已足夠。
圖中人手中拿著的那個東西就是所謂的主教冠mitre形狀。|圖源：Sam Loyd’s Cyclopedia of Puzzles (jwstelly.org)
在數學上，將正多邊形和其他簡單的幾何形狀分解成若干塊，然後重新拚成另一種形狀，叫做平面面積剖分（Dissection）。剖分可以說是拚圖遊戲的專業升級版：玩家由借助已知的碎片完成拚圖，升級到為了實現圖形的重組，自行設計和切割出合適的碎片。
剖分後來成為馬田·加德納（Martin Gardner）1961年11月在《科學美國人》上發表的「數學遊戲專欄」的主題。他在專欄里再次向公眾介紹了勞艾達馬田斯的問題——「主教冠問題」（Miter-Dissection Puzzle）。雖然讀者們踴躍參與，但沒有人能想出4塊的拚法，人們至少要把原圖形分解成5塊，才能把它們重新拚出一個正方形。
直到勞艾達馬田斯過世百餘年後的2024年5月27日，mathstodon社區一位名為Vesa Timonen的用戶貼出了下圖：
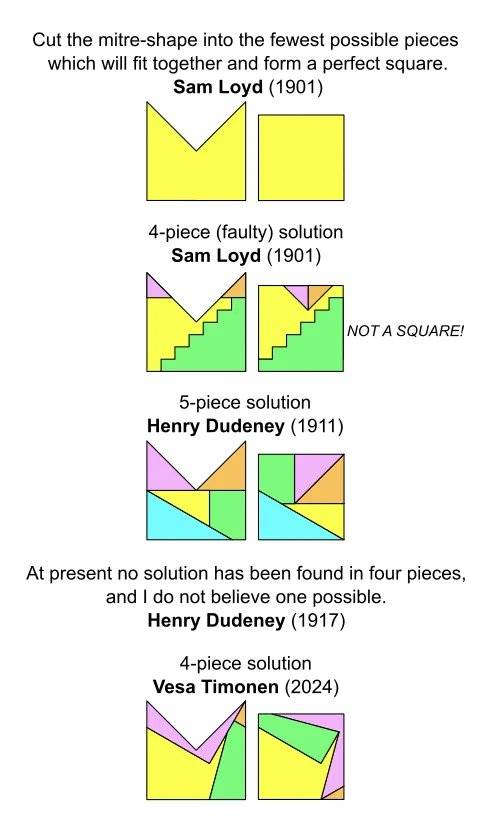圖源：vesatimonen.github.io4塊拚圖
先解釋一下圖片里的內容。
最上面一層是勞艾達馬田斯在1901年提出的問題：把左側的圖形剖分後，重新拚成右側的圖形（正方形）。
從上往下第二層是勞艾達馬田斯自己給出的解答。從圖里可以看到，他借助台階錯合的技巧，想要構造出正方形。但是，簡單計算一下就知道無法得到正方形。
第三層則是歷史上亨利·杜德尼給出的5塊剖分的構造。當然，除了杜德尼之外，還有其他人也給出了自己的5塊剖分構造，其中包括國內一位名為傅薇的摺紙和解謎高手。甚至在Vesa Timonen後來開列的參考文獻里，就包括傅薇發表在微信公眾號上的一篇文章《摺紙思路新解百年數學題》（也就是文末參考資料2，作者給出了新穎的5塊解法）。
Timonen認為傅薇的這篇文章，是在他之前對這個問題梳理得最好的文獻。雖然他看不懂中文，但是借助翻譯軟件讀完了全文。感興趣的朋友可以找來一讀，其中還有很詳細的計算，可以解釋為何勞艾達馬田斯的方法行不通。同時，由於一直找不到4塊剖分，一段時間以來，人們傾向於認為，不存在4塊的解法……
至於第四層，就是Timonen本人發現的4塊剖分解法。
想出剖分方法是很睏難的，但是驗證已有的方法則非常簡單。數學界在初步檢驗過後，就有人疑惑道：Vesa Timonen是誰啊？他又是怎麼做到的？
雙重身份
Vesa Timonen擁有雙重身份，白天按部就班地上班，幹的是令自己討厭的嵌入式軟件工程師，晚上則是才華橫溢的智力玩具謎題設計師。儘管他在數學圈子裡毫無名氣，但Timonen是芬蘭最傑出的益智玩具設計師之一，也是為數不多的拚圖設計師之一。甚至在國內的智力玩具（如巧環、魯班鎖這種）愛好者圈子裡，也有很高的知名度。
工作中的Vesa Timonen丨圖源：https://pulmallinentapaus.blogspot.com/他從小就對魔術感興趣，但是隨著年齡增長，他更願意去破解魔術。後來，他的叔叔教他玩七巧板，他們開始一個接一個地解決七巧板的難題。等成年後，他開始自己設計謎題。他的許多作品都被Hanayama Cast系列收錄。Hanayama是一家對於謎題愛好者來說非常有影響力的日本玩具公司。
Timonen認為，任何人都可以通過不斷嘗試和分析失敗來創造出獨特的謎題。他還強調，失敗是創作過程中的一部分，每次失敗都會帶來新的啟示和靈感。
智力玩具設計師的筆記本上全是幾何圖形和數學計算丨圖源：https://pulmallinentapaus.blogspot.com/
這一次，Timonen編寫了一個軟件，希望能借助現代計算機的算力系統地解決各種剖分問題。他選中的第一個問題就是主教冠問題，然後十分順利地找到了答案。實際上，如果滑動邊界，可以構造出無限多個4塊剖分解法。
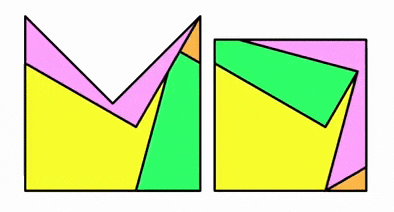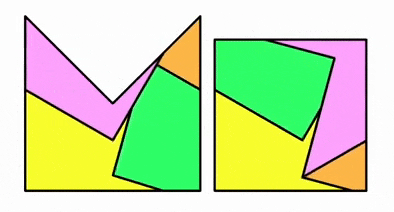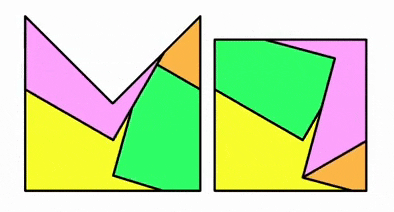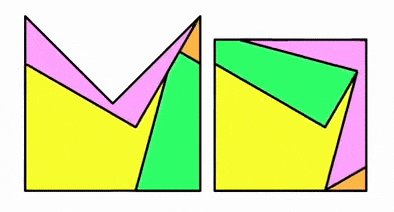
示意圖（直觀看起來圖形可能邊長不等，但實際上誤差很小） 丨圖源：THE MITRE DISSECTION PUZZLE (vesatimonen.github.io)
南韓延世大學的數學博士Jin-Hoo Ahn為Timonen的解法提供了一個無文字證明，大家可以欣賞一下。
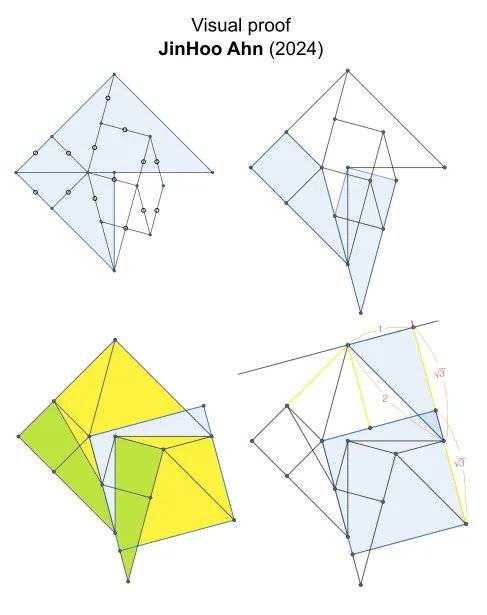圖源：THE MITRE DISSECTION PUZZLE (vesatimonen.github.io)稍帶一提，Jin-Hoo Ahn也是謎題愛好者，還會製造機關盒一類的智力玩具。或許就是因此和本文的主角有了交集。
更加數學
Timonen的4塊剖分解里，有一個瑕疵：兩邊的綠色塊其實是鏡像對稱的。也就是說，拚圖的時候，綠色塊沒有區分正反面。Timonen嘗試尋找不包含鏡像對稱的剖分方法，但始終未能成功。相反，程序找到了50多個不帶鏡像對稱的5塊解法。所以，或許並不存在4塊非鏡像的剖分解法，但我們還未能證明這一點。這也是這道百年謎題所缺失的最後一塊拚圖。
在數學上，我們有著名的華勒斯-波埃伊-格維也納定理（Wallace-Bolyai-Gerwien Theorem，1807）：對於任意兩個多邊形，都可以把其中一個分割成有限多個小多邊形，並經過平移和旋轉，拚合成第二個大多邊形。
上述定理保證了剖分的可行性，但是當把「有限個」限制到具體的數值時（比如說今天的問題是4塊），就無法保證僅靠平移和旋轉就能拚合成功。翻轉小塊得到鏡像，或許是必要的操作。
除了限制翻轉-鏡像的使用之外，人們有時對剖分加上一些更強的限制。如著名的鉸接式剖分Hinged dissection。
在幾何中，鉸接式剖分（又稱擺動鉸鏈式剖分或杜德尼剖分）的所有部分都通過「鉸鏈」的接點連成整體。如此一來，從一個圖形到另一個圖形的重新排列可以通過連續擺動鏈來進行，而不會（也不能）切斷任何連接。通常情況下，我們假定在摺疊和展開過程中允許碎片重疊。
鉸接式剖分的概念是由前文提到的亨利·杜德尼推廣的。他在1907年出版的《簡迪伯雷謎題》（The Canterbury Puzzles）一書中，介紹了著名的將正方形用鉸鏈剖成三角形的方法。
圖源：Hinged dissection – Wikipedia然而，是否能把華勒斯-波埃伊-格維也納定理推廣到鉸接式剖分上呢？亦即兩個面積相等的多邊形，是否必然能通過一個鉸接式剖分化為彼此？這個問題一直懸而未決。
直到2007年，Erik Demain等人證明了必定存在這樣的鉸接式剖分，並提供了一種生成鉸接式剖分的構造算法。即使要求擺動時組件不會重疊，這個證明也是成立的，而且可以推廣到任何一對有共同剖面的三維圖形。然而，在三維空間中，並不能保證組件重組時不會彼此重疊。二維平面上重疊的話，在物理上是很容易實現的——只要理解成運動過程中分出上下兩層便可。但是三維構件彼此重疊，則是物理上的剛體無法實現的。只能當成是數學上的無實體對象。
化圓為方
前面的討論始終停留在直線構成的圖形上，那麼，由曲線圍成的圖形也能剖分重組嗎？或許最終極的剖分問題，就是化圓為方。
公元前450年左右，相信「理性統治世界」的哲學家、天文學家和數學家Anaxagoras，在因瀆神而遭遇監禁的期間提出了一個現在著名的數學問題，即：僅使用圓規和沒刻度的直尺，你能畫出一個與給定圓等面積的正方形嗎？
這個問題在1882年有了答案，當時德國數學家費迪南·馮·林德曼（Ferdinand von Lindemann）證明，這是一個尺規作圖不能問題。他證明圓週率π是一種特殊的數字，稱之為超越數（超越數還包括e）。
原本故事可以在這裏畫上句號。但在1925年，人類歷史上最重要的邏輯學家之一的阿爾費特·塔斯基（Alfred Tarski）通過調整規則重新提出了這個問題。他問，是否可以通過將一個圓盤切成有限數量的小塊，用它們重新拚出一個正方形來？
1988年，Miklós Laczkovich正面回答了塔斯基的問題：圓形可以剖分後重新配置為正方形，大概需要把圓分解成1050個碎片。但是相當長的一段時間以來，化圓為方的剖分方法里總是涉及一些無法直觀展示和可構造的成分：存在面積無法定義（勒比格不可測集）的碎片和麵積為0的碎片（零測度集）。
直到前幾年，加州大學洛杉磯分校的數學家Andrew Marks與現在在多倫多大學的Spencer Unger才提供了第一個完全構造性的化圓為方的證明：每個碎片都有明確的面積，無一例外。
代價是，他們要把圓分解成10200個碎片，同時雖然理論上是可構造的，但過程太複雜，無法進行展示。
2022年2月，華威大學的Andras Máthé和Oleg Pikhurko以及Victoria大學的Jonathan Noel在網上發表的一篇論文為這一古老的問題添加了新的內容。他們的作品雖然也把圓分為約10200塊，但形狀更簡單，更容易形象化。甚至可以做成演示影片（見文末參考[9]）。
數學家已經有了進一步簡化拚圖碎片的想法，減少總數和不均勻性。Marks做過的計算機模擬實驗表明——但未證明——分解可以至多用22塊來完成。他認為最低數字可能會更低。
「我敢打賭，你可以用不到20塊來化圓為方。」他說，「但我不會賭上1000美元。」
參考資料
[1]Sam Loyd’s Cyclopedia of Puzzles(jwstelly.org)
[2]摺紙思路新解百年數學題(qq.com)
[3]THE MITRE DISSECTION PUZZLE(vesatimonen.github.io)
[4]Pulmallinen tapaus：Vesa Timonen訪談
[5]Hinged dissection-Wikipedia
[6]An Ancient Geometry Problem Falls to New Mathematical Techniques|Quanta Magazine
[7]Dissection–from Wolfram MathWorld
[8]Vesa Timonen:”Dissecting a mitre.#dissectio…”-Mathstodon
[9]度量幾何演示塔斯基化圓為方問題的解_嗶哩嗶哩_bilibili
本文來自微信公眾號：返樸 （ID：fanpu2019），作者：嘉偉
