首個o1複現開源RL框架OpenR來了,UCL、上交等高校聯合團隊發佈
AIxiv專欄是機器之心發佈學術、技術內容的欄目。過去數年,機器之心AIxiv專欄接收報導了2000多篇內容,覆蓋全球各大高校與企業的頂級實驗室,有效促進了學術交流與傳播。如果您有優秀的工作想要分享,歡迎投稿或者聯繫報導。投稿郵箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
OpenR 研究團隊成員包括:汪軍教授,倫敦大學學院(UCL)計算機系教授,阿倫・圖靈研究所 Turing Fellow,其指導的 UCL 一年級博士生桑治研。利物浦大學助理教授方蒙。上海交通大學 Apex 和多智能體實驗室張偉楠教授(上海交通大學計算機系教授、博士生導師、副系主任),溫穎副教授(上海交通大學約翰・霍普克羅夫特計算機科學中心副教授)以及其指導的博士生萬梓煜、溫睦寧、朱家琛。張偉楠教授和溫穎副教授博士期間就讀於 UCL,指導教師為汪軍教授。香港科技大學(廣州)創校校長,倪明選(Lionel M. Ni),香港工程科學院院士,香港科技大學(廣州)講席教授。陳雷,香港科技大學(廣州)信息樞紐院長,講席教授。香港科技大學(廣州)一年級博士生劉安傑、龔子欽受汪軍教授和楊林易博士聯合執導,以及西湖大學工學院助理教授(研究)楊林易。
o1 作為 OpenAI 在推理領域的最新模型,大幅度提升了 GPT-4o 在推理任務上的表現,甚至超過了平均人類水平。o1 背後的技術到底是什麼?OpenAI 技術報告中所強調的強化學習和推斷階段的 Scaling Law 如何實現?
為了嘗試回答這些問題,倫敦大學學院(UCL)、上海交通大學、利物浦大學、香港科技大學(廣州)、西湖大學聯合開源了首個類 o1 全鏈條訓練框架「OpenR」,一個開源代碼庫,幫助用戶快速實現構建自己的複雜推斷模型 。整個項目由 UCL 汪軍教授發起和指導,實驗主要由上海交大團隊完成。

我們介紹了 OpenR,首個集過程獎勵模型(PRM)訓練、強化學習、多種搜索框架為一身的類 o1 開源框架,旨在增強大型語言模型(LLM)的複雜推理能力。
-
論文鏈接:https://github.com/openreasoner/openr/blob/main/reports/OpenR-Wang.pdf
-
代碼鏈接:https://github.com/openreasoner/openr
-
教程鏈接:https://openreasoner.github.io/
OpenR 將數據獲取、強化學習訓練(包括在線和離線訓練)以及非自回歸解碼集成到一個統一的平台中。受到 OpenAI 的 o1 模型成功的啟發, OpenR 採用了一種基於模型的方法,超越了傳統的自回歸方法。我們通過在 MATH 數據集上的評估來展示 OpenR 的有效性,利用公開的數據和搜索方法。初步實驗表明,相對改進達到了顯著提升。我們開源了 OpenR 框架,包括代碼、模型和數據集,我們旨在推動推理領域開源社區的發展,歡迎感興趣的從業人員加入到我們的開源社區。代碼、文檔、教程可通過 https://openreasoner.github.io 訪問。
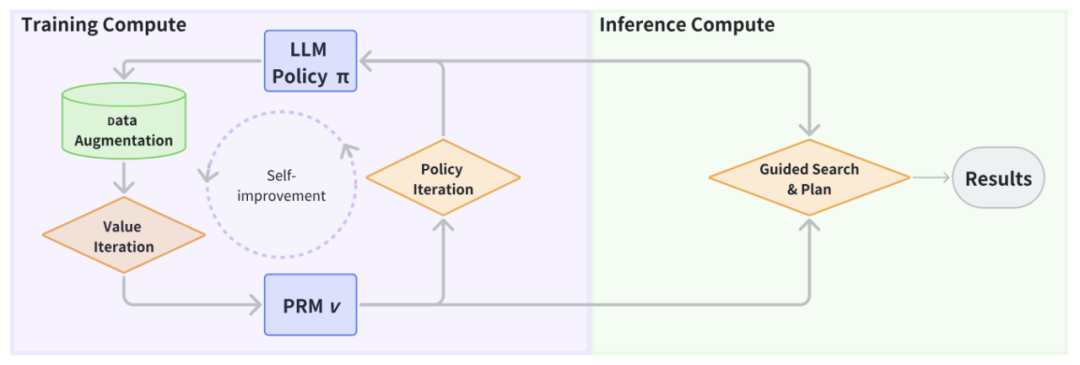
圖 1: 系統設計圖
系統設計。過程獎勵模型 (PRM) 在兩個關鍵方面增強了 LLM 的策略。首先,在訓練期間,PRM 通過策略優化技術(如上圖所示的策略迭代)改進 LLM 策略。其次,在解碼階段,PRM 引導 LLM 的搜索過程,使推理朝著更有效的結果發展(如上圖所示)。接下來我們將展示,LLM 策略還可以幫助識別缺失的中間推理步驟,這反過來又可以進一步訓練和改進 PRM。正如上圖所示,這種迭代的互動使 LLM 和 PRM 能夠持續地釋放各自的潛力以改進推理。


圖 2 代碼結構圖
數據增強.在使用 LLM 進行推理時,我們不僅僅依賴最終答案的反饋,而是使用更詳細的反饋方式,逐步收集和標註數據。這樣可以在問題解決的過程中,識別出具體的錯誤位置並給出反饋,從而幫助模型更好地學習和改進。
MATH-APS.我們通過自動生成合成樣本來增強數據。與依賴昂貴且難以擴展的人工標註的 PRM800k 數據集不同,我們引入了一個新數據集 MATH-APS。這個數據集基於 MATH 數據集,並使用 OmegaPRM 等自動化方法來生成樣本,從而減少了對人工標註的依賴,更易於大規模收集數據。自動化方法如 OmegaPRM、Math-Shepherd 和 MiPS 可以高效地收集高質量的過程監督數據。雖然 Math-Shepherd 和 MiPS 提供了過程監督的自動化標註,但它們需要大量的策略調用,計算成本較高。OmegaPRM 改進了這個過程,通過迭代地劃分解決方案、回溯分析並找出模型推理中的第一個錯誤步驟來提高效率。
我們通過自動生成合成樣本來增強數據。與依賴昂貴且難以擴展的人工標註的 PRM800k 數據集不同,我們引入了一個新數據集 MATH-APS。這個數據集基於 MATH 數據集,並使用 OmegaPRM 等自動化方法來生成樣本,從而減少了對人工標註的依賴,更易於大規模收集數據。自動化方法如 OmegaPRM、Math-Shepherd 和 MiPS 可以高效地收集高質量的過程監督數據。雖然 Math-Shepherd 和 MiPS 提供了過程監督的自動化標註,但它們需要大量的策略調用,計算成本較高。OmegaPRM 改進了這個過程,通過迭代地劃分解決方案、回溯分析並找出模型推理中的第一個錯誤步驟來提高效率。
PRM 的監督訓練。在過程獎勵模型 (PRM) 中,主要目的是判斷解決方案的步驟是否在正確的軌道上。因此,PRM 會輸出一個 0 到 1 之間的分數,作為當前解決過程的正確性指標。具體來說,給定一個問題及其解決步驟序列,PRM 會為每一步計算出一個分數,這可以視為一個二元分類任務:是否正確。我們通過在大型語言模型 (LLM) 上的監督微調來訓練 PRM,將正確或錯誤的判定作為分類標籤,並進一步使用 LLM 來預測每一步的後續標記。
Math-psa PRM 通過在 LLM 上的監督微調來訓練,正確 / 錯誤的區分作為分類標籤。我們使用數據集如 PRM800K,Math-Shepherd 以及我們自己的 MATH-APS 數據集來訓練一個名為 Math-psa 的 PRM。這些數據集由三個部分組成:問題、過程 和 標籤。輸入由 問題 和 過程 的拚接組成。在 過程 中,解決方案被分為多個步驟,每個步驟用一個特殊的步驟標記分隔,以標記每個步驟結束的位置,PRM 可以在此處進行預測。標籤對整個過程進行分類,根據解決方案的正確性將每個步驟標記為 + 或 -。
在訓練過程中,模型會在每個步驟標記之後預測正或負標籤。輸入的拚接格式包含了 問題 和各個步驟之間的標記符。標籤僅分配在步驟標記符的位置,並在計算損失時忽略其他位置。這種方式確保模型訓練時主要關注輸入序列,而不會被步驟標記符干擾,從而更好地識別和分類正確性。
LLM 的策略學習。我們將數學問題轉換為一個語言增強的決策過程,用來逐步解決問題。這個過程叫做馬爾可夫決策過程 (MDP),它由狀態、動作和獎勵組成。在這個框架中,每一個數學問題就是初始狀態,模型生成推理步驟作為動作,然後根據當前狀態和動作來決定下一個狀態。
模型每完成一個步驟,就會得到一個獎勵或反饋,用來評估該步驟是否正確。這個獎勵幫助模型判斷是否朝著正確方向前進。整個過程重覆進行,模型會不斷調整其推理路徑,目標是獲得儘可能多的正面反饋或獎勵。
我們將這種 MDP 實現為一個強化學習環境,類似 OpenAI 的 Gym 環境。在這裏,每個數學問題都被看作一個任務,模型通過一系列連續的推理步驟來解決這些問題。正確的步驟獲得獎勵,錯誤的步驟則受到懲罰。通過這種方式,模型可以在不斷試錯中優化其策略,從而逐漸提高其解決數學問題的能力。
在線強化學習訓練。在使用強化學習訓練大型語言模型 (LLM) 時,通常使用近端策略優化 (PPO) 來使生成的語言輸出與預期的動作對齊。PPO 可以幫助模型生成既符合語境又達到目標的響應,填補了語言理解和操作輸出之間的空隙。我們提供了傳統的 PPO 和一種更高效的變體,即群體相對策略優化 (GRPO)。這兩者主要在優勢值的計算方法上不同:PPO 使用一個網絡來估算狀態值,並通過廣義優勢估算 (GAE) 技術來計算優勢值;而 GRPO 則簡化了這個過程,直接使用標準化的獎勵信號來估算動作的優勢,從而減少了訓練資源的消耗,同時更加註重獎勵模型的穩定性。
解碼:推理時的引導搜索和規劃
我們使用 PRM 來評估每個解決步驟的準確性。一旦訓練出高質量的過程獎勵模型,我們就可以將其與語言模型結合到解碼過程中,從而實現引導搜索和多次生成的評分或投票。
為了將 PRM 用作驗證器,我們定義了評估 LLM 生成的解決方案正確性的方法,將每一步的得分轉換為最終分數。主要有兩種方法:
-
PRM-Min:選擇所有步驟中得分最低的作為最終分數。
-
PRM-Last:選擇最後一步的得分作為最終分數。這種方法已經被證明效果與 PRM-Min 相當。
當通過擴大推理時計算生成多個答案後,我們需要基於分數選擇最佳答案。我們採用了三種策略:
1. 多數投票:通過統計出現最多的答案作為最終答案。
2. RM-Max:根據結果獎勵模型,選擇最終獎勵最高的答案。
3. RM-Vote:根據結果獎勵模型,選擇獎勵總和最高的答案。
通過結合這些策略,可以形成多種加權方法,例如 PRM-Last-Max,即使用 PRM-Last 和 RM-Max 組合進行選擇。我們的框架允許我們在多種搜索算法中進行選擇,例如 Beam Search、Best-of-N, 蒙地卡羅樹搜索等。每種算法在 PRM 的質量上有其獨特的優勢。複雜的搜索算法在處理更難的任務時可能表現更好,而簡單的方法如最佳 N 則常能在難度較低的情況下表現良好。
解碼階段的 Scaling Law
我們觀察到了和 OpenAI o1 以及 Deepmind 論文《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters》趨勢相近的 Test-time Scaling Law,參見:
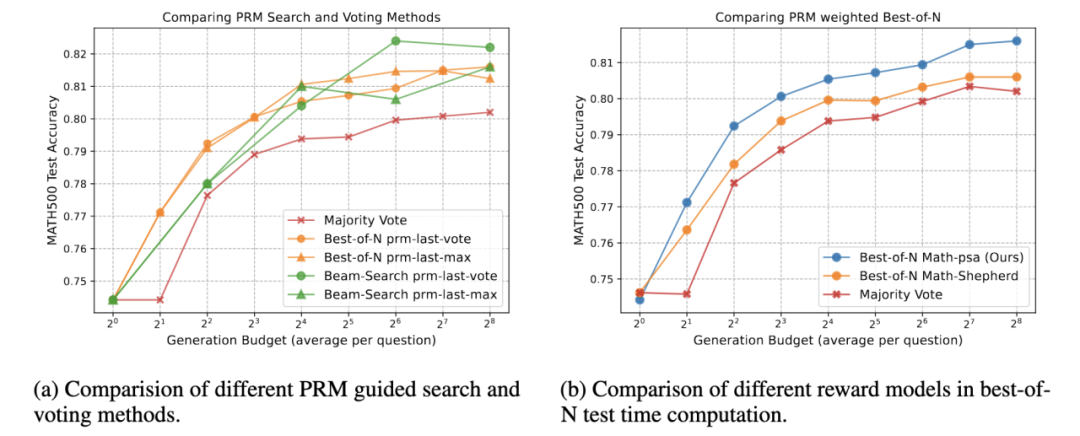 圖 3 推斷階段新的縮放率實驗效果圖
圖 3 推斷階段新的縮放率實驗效果圖圖 3 (a) 比較了這些搜索和投票方法在推理過程中的性能。y 軸表示 MATH500 數據集上的測試準確率,而 x 軸顯示生成預算(每個問題的平均標記數),反映了每個問題的計算消耗或標記使用情況。該圖表明,隨著生成預算的增加,最佳 N 選擇和束搜索方法的性能顯著優於多數投票,與之前的發現表現出相似的模式。在低推理時計算預算下,最佳 N 選擇方法表現優於束搜索,而束搜索在較高預算下可以達到相同的性能。另一方面,圖 (b) 顯示我們的 PRM (Math-aps) 能在所有測試的計算預算下達到最高的測試準確率。這確實驗證了我們的 PRM 訓練能夠有效地學習過程監督。
詳細的文檔結束。OpenR 支持使用幾行代碼即可實現 PRM 的訓練、強化學習訓練,以及不同的解碼方法,使用戶能夠方便地進行實驗和測試。我們還提供了詳細的代碼文檔供大家參考,參見: https://openreasoner.github.io/ 。我們所支持的算法如下圖所示:
 圖 4 開源代碼算法實現框圖
圖 4 開源代碼算法實現框圖 圖 5 OpenR 技術文檔圖
圖 5 OpenR 技術文檔圖










