「民主」的神經網絡:向不完美妥協
本文來自微信公眾號:神經現實 (ID:neureality),作者:楊閏哲,編輯:EON,題圖來自:AI生成
就像人類社會的運轉需要一套共同的決策規則,大腦的運轉也依賴於神經元之間的某種契約。自上世紀40年代起,理論神經科學家就試圖通過數學模型,解釋神經元活動背後隱含的「民主規則」:McCulloch-Pitts模型是鼓掌通過式的民主,Linear Threshold模型是佐治·奧威爾式的民主,Hubel和Wiesel提出了神經元民主的層級結構——在視覺系統里有好脾氣的「簡單公民」和壞脾氣的「複雜公民」。
「民主」的神經元模型是簡陋的,它不是生物大腦運作的真實方式,而是一種非常粗略的近似;但「民主」的神經元卻又是簡單高效的,它們構建了今天深度學習技術的基礎。「民主」的神經網絡似乎印證了丘吉爾的那句名言,「民主是最糟的政體,除了其它那些已經試過的不能用的之外。」
世界上最熱鬧的「社交網絡」,就在你頭腦里
在我們小小的顱腔里住著860億個神經元,它們有的易燃易怒,脾氣暴躁;有的鬱鬱寡歡,消極厭世;它們每天都在對我們經歷的事物各抒己見,爭吵不休。如果你不能想像大腦里每天沸沸揚揚的辯論實況,那就想一想微博或Twitter——一個不過月活3、4億用戶的社交網絡——每天是如何製造熱點、生產和傳播假新聞、或者粉圈互撕到服務器宕機的。
我們的大腦規模約等於二十多個這樣的社交網絡,平均每個用戶有1000位粉絲。而且這些用戶活躍時戰鬥力非凡,平均每個神經元3至4秒就發一次推,大腦短短一小時產生的信息足以淹沒任何超話熱搜。
即使是一個平日裡看起來非常好脾氣的人,他的大腦中也充滿了不間斷的爭執。舉例來說,即使像是「看到一塊芝士蛋糕」這樣一個簡單、統一的事件單位,也是大腦中成千上百的神經元激烈辯論的結果。每個參與其中的神經元——從視網膜,到視覺皮層,再到下顳葉——通過產生動作電位、釋放神經遞質來發表見解。
神經元們似乎總是很難達成一致,比如視網膜中的雙極神經元(bipolar cells)往往樂於表達讚同,讓其他神經元更加興奮,而無長突細胞(amacrine cells)總是悲觀否定,抑制其他神經元的活動。但無論如何,這些常常意見相左的神經活動終究會彙總成一個明確的、無可辯駁的概念,並讓我們不禁嚥了嚥口水。
不僅僅是簡單的「刺激-反應」過程,神經科學家們相信,我們所有的情感、記憶、思考和創造,都是這群吵吵鬧鬧的「烏合之眾」的共同決定。它們是如何做到的?
兩個原則:經驗就是動作電位的模式,學習就是突觸連接的改變
把大腦看作一個網絡,並非一個新鮮的概念。早在社交網絡的概念尚未發明的20世紀40年代,科研人員就試圖用網絡模型解釋大腦的運作機制。在這類模型中,大腦被看作一幅只有節點和連邊的計算圖,網絡中的每一個節點像征一個神經元,每一條連邊象徵著兩個神經元之間的突觸連接,信息在網絡中有向地從一個節點流向另一個節點,分佈式地在每個節點被計算和處理。
比如在小鼠的大腦中,每個神經元從樹突接受來自其他神經元的電信號,在胞體上進行計算,再從軸突通過動作電位把計算結果發送給其他神經元。
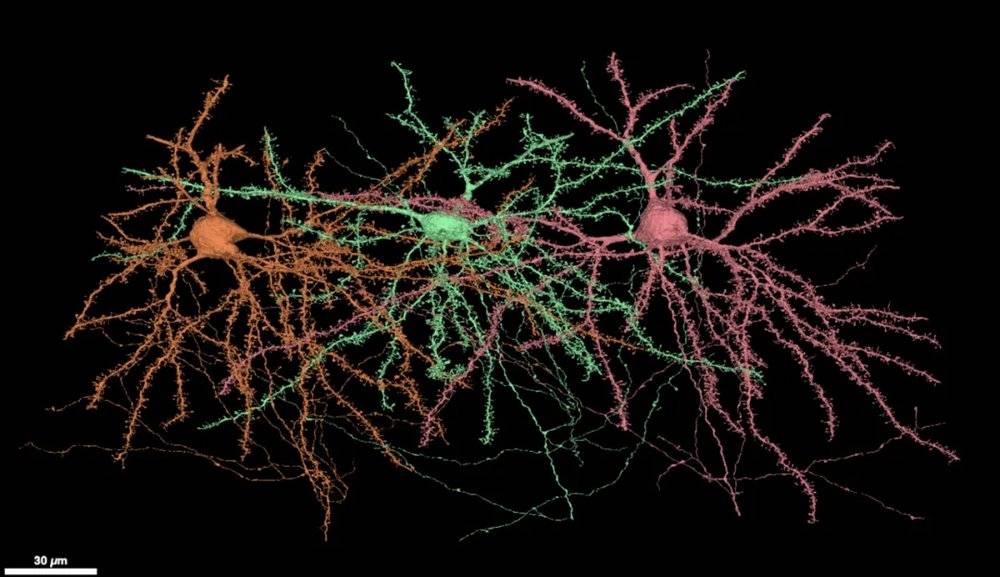
小鼠視覺皮層L2/3中的三個興奮性神經元。圖中較粗有許多凸起的枝幹為神經元的樹突,(底部)較細較光滑的枝幹為神經元的軸突。
來源:MICrONS Explorer,https://microns-explorer.org/phase1
為了把這類計算模型和大腦的認知功能聯繫起來,神經科學家們提出了兩個普遍接受的原則:
我們所有豐富的內部體驗和外部活動,不過是神經元持續的動作電位模式。
我們從過去經驗中學習的能力,大多歸功於神經元之間突觸連接的可塑性。
這兩個原則,在大腦的結構和功能之間搭起一座橋樑。只要知道神經元之間的突觸連接,我們就可以從某種程度上解釋大腦是如何一步一步地處理信息的。不同的局部連接結構賦予了大腦不同的功能;這些結構中持續的電信號,構成了我們的行為和體驗,比如速記一串電話號碼;這些突觸連接的動態變化,給予了認知系統迭代進步的能力,比如學習新技能。
謝靈頓反射弧(Sherrington‘s reflex arc)可能是最早把突觸連接和功能聯繫起來的模型,可以被視作最早的「神經網絡」。動物反射行為通常由從感覺神經元到運動神經元的一系列突觸鏈執行,這種特殊的鏈狀神經結構被叫做反射弧。
一個完整的反射弧通常包括五部分:感受器負責從環境接受信息,傳入神經將信息傳導至神經中樞,再由傳出神經將反應返回到效應器。如果用計算圖表示,反射弧就是一個包含五個節點的路徑,每個節點被激活的順序反映了刺激到反應的一系列因果關係。
「現代神經科學之父」卡哈爾(Santiago Ramón y Cajal)的學生德諾(Rafael Lorente de Nó)提出了循環的突觸連接可能是中樞神經系統的基本結構。和反射弧的開放結構不同,突觸環(synaptic loops)是一條閉合的鏈,從而使神經活動的模式得以保持。
謝靈頓的學生格拉咸·布朗(Graham Brown)在研究脊髓的節律性時也提出,一些神經活動有可能在大腦的內部生成,而不依賴於即時的刺激-反應關係。反射弧在被外界刺激之前是不活躍的,但是因為環狀突觸結構和內部生成的神經活動,大腦的活動可以不依賴於外界刺激。
進一步,唐納德·赫布(Donald Hebb)在1949年提出的「細胞集結理論」(cell assembly theory)認為不同的神經元集群構成了神經系統的基本功能單元,並討論了突觸可塑性的形式。神經元之間反復的突觸通訊,可以強化它們之間的連接,從而形成德諾說的能夠保持神經活動的突觸環。
赫布、德諾、布朗、謝靈頓等人的想法,最終通過數學抽像為神經網絡。最著名的兩類基本模型,就是感知機(perceptrons)和聯想記憶網絡(associative memory networks)。感知機模型常常被用來解釋視覺系統是如何識別物體,而聯想記憶網絡則試圖解釋大腦是如何存儲和提取信息的。
1957年由科蘭克·羅森白禮達(Frank Rosenblatt)提出的感知機模型,是對謝靈頓反射弧概念的數學抽像與推廣。和反射弧一樣,信息在網絡中的流動也是單向的,即從輸入到輸出。但與反射弧不同的是,感知機允許許多輸入彙聚到單個神經元,也允許單個神經元有多個輸出。感知機也可以看作是單層的前饋神經網絡(feedforwad networks)。在前饋神經網絡中,突觸連接不允許形成環鏈。
聯想記憶網絡往往帶有回路和環鏈,今天被歸類為循環神經網絡(recurrent networks)或者回饋神經網絡(feedback networks)。而感知機模型則非常適用於研究大腦對外界刺激的即時響應。在人工智能技術大行其道的今天,用於圖像識別的人工神經網絡,多數類似於原始的感知機模型;而用於閱讀理解的網絡,則往往包含了許多循環結構來維持工作記憶。
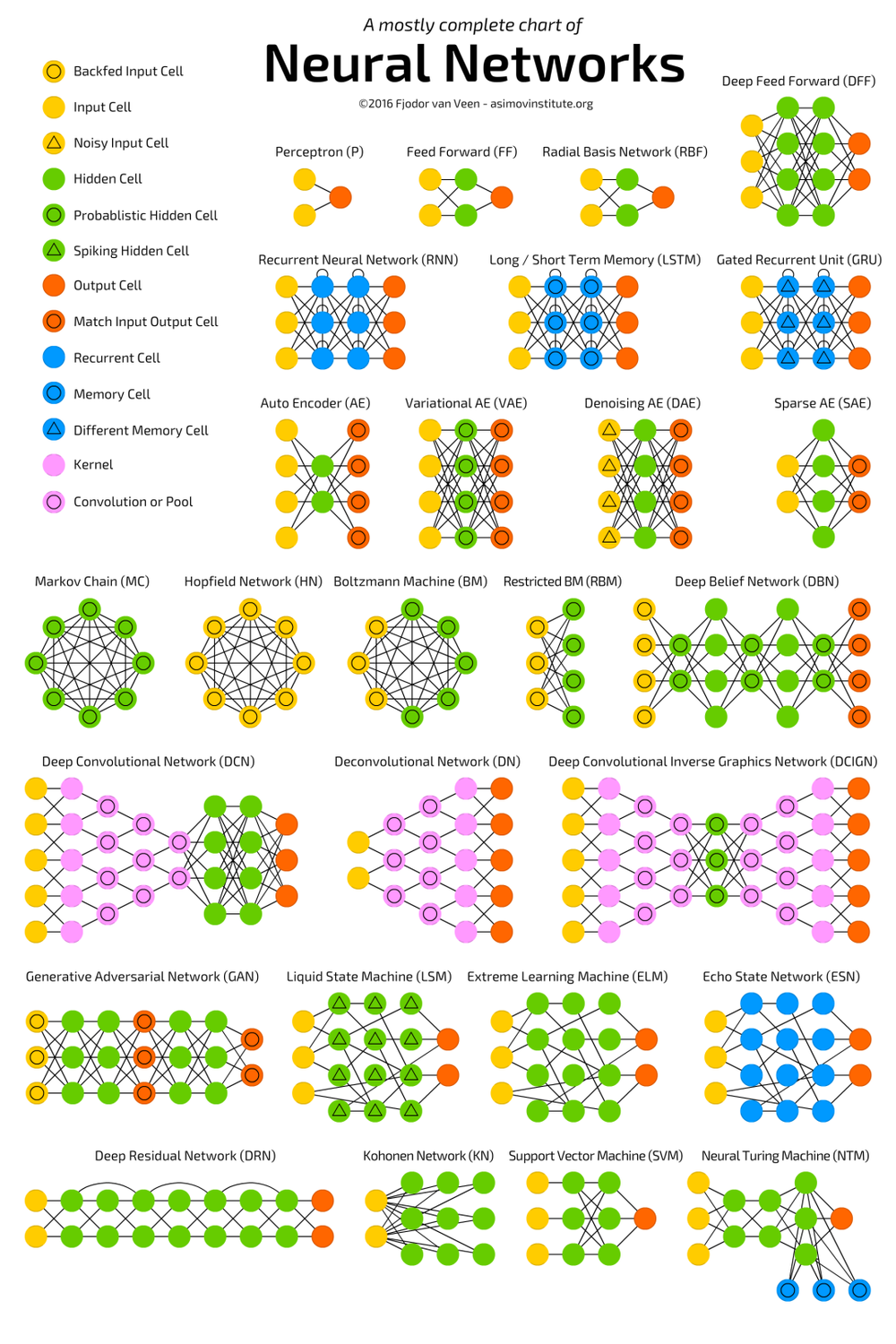
百花齊放的人工神經網絡模型,大多模型都是從感知機和聯想記憶網絡演化而來。
來源:Fjodor van Veen,https://towardsdatascience.com/the-mostly-complete-chart-of-neural-networks-explained-3fb6f2367464
兩條原則——經驗就是動作電位的模式,學習就是突觸連接的改變——使得通過模擬神經網絡來實現認知功能的聯結主義人工智能變得充滿希望。計算機科學家與神經科學家們相信,無論多複雜的功能,都可以從龐大的神經網絡中湧現,只要找到了對的突觸連接方式。
深度學習技術成功的關鍵,就是運用第二條原則來找到執行特定功能的神經網絡。雖然今天計算機科學家們使用的更新突觸連接的算法,和神經科學家普遍發現的赫布法則非常不同。
關於第二條原則的討論我們可能需要另一篇文章來展開。而今天這篇文章會試圖向你證明,單單第一條原則可能已經足夠有趣。作為經驗載體的動作電位是如何在神經網絡中計算與傳播的?網絡中的一個神經元常常從與之相連的一眾神經元接聽信息,這些吵鬧的神經元常常有著非常不同的神經活動和突觸電位,神經元是如何整合這些不同意見的?
一人一票製:民主決策的基石
神經元的動作電位和突觸電位是時刻變化的,它們涉及到膜電壓和離子通道開閉之間的複雜相互作用。為了建模每個神經元的行為,理論神經科學家有時會忽略其中的這些複雜性。
一種非常流行的簡化是,當同時激活的興奮性突觸數量足夠時,神經元就會激發動作電位。這一簡化是合理的,因為單個興奮性突觸後電位(excitatory postsynaptic potential)通常比激發動作電位所需的電壓差小很多。因此,突觸後神經元的胞體需要對同時激活的那些興奮性突觸後電位求和,使得其總電壓有可能超過激發閾值。
1943年,沃倫·麥卡洛克(Warren McCulloch)和禾達·皮茨(Walter Pitts)為這種對動作電位求和的神經元建立了數學模型。McCulloch-Pitts神經元同時接受多個輸入並產生單個輸出(但可能發送給多個神經元)。神經元輸入和輸出都用二元變量0或1表示,0為沉默,1為活躍。每個神經元都有一個閾值參數θ,表示激發神經元所需的最小興奮性突觸數量。如果在某一時刻的輸入總和大於或等於θ,則神經元的輸出為1;否則輸出為0。
我們可以連接多個這樣的McCulloch-Pitts神經元,使得一個神經元的輸出就是另一個神經元的輸入。這一簡單的數學過程也有對應的生物解釋:突觸前神經元的放電可以激活另一個神經元上的突觸後電位。把許多這樣的McCulloch-Pitts神經元連接在一起,我們就構建了一個神經網絡。
比上述的0和1稍稍複雜一些,最初的McCulloch-Pitts神經元同時考慮了興奮性和抑制性突觸的存在。類似一套民主投票規則,興奮性突觸的1記一張讚成票,抑制性突觸的1記一張反對票,0為棄權票。所有突觸前的神經元都可以表達它們的意見,突觸後神經元彙總這些意見再進行決策。
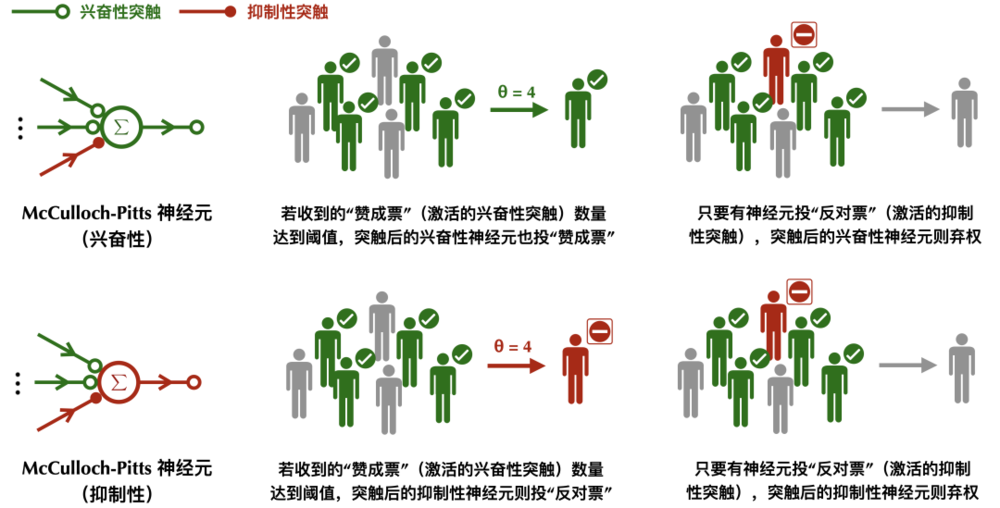 McCulloch-Pitts神經元的工作原理:興奮性突觸一人一票,抑制性突觸一票否決。
McCulloch-Pitts神經元的工作原理:興奮性突觸一人一票,抑制性突觸一票否決。如果突觸後的神經元是興奮性的,那麼它屬於神經網絡中那一類持有樂觀立場投票者,只會投讚成或者棄權票;相反如果突觸後的神經元是抑制性的,那麼它屬於悲觀的且特立獨行的投票者,只會投反對票或者棄權票。
這一限制遵循了神經科學中稱為戴亞法則(Dale‘s principle)的規律,一個神經元只會向其他的神經元分泌相同的神經遞質,從而形成要麼興奮性要麼抑制性的突觸。雖然今天神經學家已經發現了許多戴亞法則的反例,但是在大部分情況下,這一規律還是有普遍性的。
在McCulloch-Pitts模型中,對於興奮性的神經元,如果它收到的來自其他神經元的「讚成票」(激活的興奮性突觸)數量達到某個閾值,比如超過半數,並且沒有神經元向它投「反對票」,它就會向與之相連的其他神經元投「讚成票」(1),否則棄權(0);
對於抑制性的神經元,如果它收到的來自其他神經元的「讚成票」(激活的興奮性突觸)數量達到某個閾值,並且沒有神經元向它投「反對票」,它就會向與之相連的其他神經元「反對票」(1),否則棄權(0)。如果一個神經元收到了「反對票」(有抑制性突觸被激活),那麼無論神經元本身是興奮性還是抑制性,都會投棄權票(0)。
McCulloch-Pitts模型可以看作一種「鼓掌通過」式的民主,只要投讚成票的興奮性神經元超過一定數量,就可以激發突觸後神經元作出決定。同時,抑制性的神經元還具有「一票否決」權,只要它對刺激不滿意,它就可以使下遊的神經元不響應。
在這種體制中,每個神經元唯一需要關心的變量就是投票通過的閾值。低閾值的神經元像是人群中極易被煽動的壞脾氣,只要有少量神經元衝它發火,它也會跟著發火;而高閾值的神經元則木訥許多,需要大量神經元同時對它苦口婆心地勸說,它才會審慎地投出自己寶貴的一票。
這種民主制度雖然簡單粗暴,但已經可以解決許多複雜問題。我們在後面會介紹到,低閾值的興奮性McCulloch-Pitts神經元相當於邏輯電路中的「與門」,高閾值的興奮性McCulloch-Pitts神經元相當於邏輯電路中的「或門」,而抑制性神經元的作用和「非門」類似。一個由McCulloch-Pitts神經元構成的網絡,在某種程度上等價於一個邏輯電路。我們的視覺系統也可以從類似的角度被解釋。
McCulloch-Pitts是最簡單的神經元模型,但它也缺失了許多重要的生物細節。其中最值得注意的一點是,在McCulloch-Pitts模型中,所有的興奮性輸入是被同等對待的。如果激活,則記為一票,每一票都同等重要。神經元的「身份」在這一民主機制中被完全革除了。
而真正的生物神經元並非能做到如此絕對公平公正。神經元之間往往會形成不同強度的突觸。這意味著突觸後神經元會有意地更重視某些神經元的意見,而輕視另外一些。
將突觸強度的差異性納入考慮的神經元模型,叫做線性閾值神經元(Linear Threshold neurons)。和McCulloch-Pitts模型一樣,它也遵循了民主最基本的一人一票原則,記活躍為1,沉默為0,只是有的突觸在最終計票時會被賦予更高的權重。這更像是《動物莊園》式的民主,「所有神經元生來平等,但有的神經元比其他神經元更平等」。只有當來自所有突觸的投票的加權和大於或等於預設的某個閾值θ,突觸後的神經元則被激活。
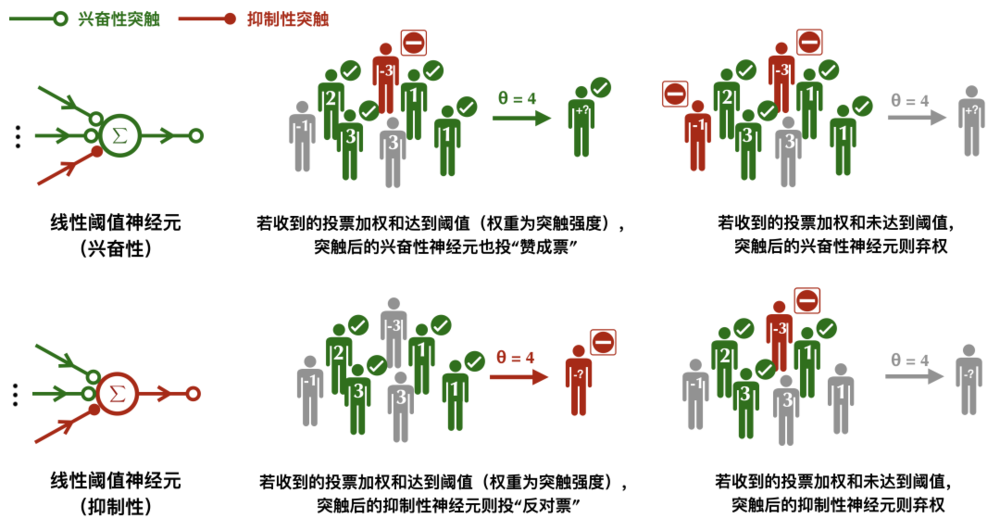 線性閾值神經元的工作原理:興奮性的突觸擁有正權重,抑制性突觸擁有負權重,投票結果由加權和決定。
線性閾值神經元的工作原理:興奮性的突觸擁有正權重,抑制性突觸擁有負權重,投票結果由加權和決定。此外,在線性閾值神經元模型中,抑制性神經元不再有一票否決權。相反它採取了一種更加公平的做法,興奮性的突觸擁有正權重,抑制性突觸擁有負權重,只有當來自興奮性突觸的聲音蓋過了那些抑制性突觸,並達到閾值,突觸後神經元才會被激活。
McCulloch-Pitts模型可看作一種興奮性突觸權重均為1的線性閾值神經元。而要讓抑制性神經元像在McCulloch-Pitts模型中那樣可以「獨裁」,只需把抑制性突觸的權重設為興奮性突觸總數的相反數。
無論是McCulloch-Pitts神經元還是線性閾值神經元,都只刻畫了神經元活躍(1)與不活躍(0)兩種狀態。而生物神經元的放電速率是連續分級的。
另外,在線性閾值神經元中,神經元的輸入是電流強度(假設突觸強度與神經元活動相乘得到電流),輸出是放電速率,這意味著胞體在進行一種將輸入電流轉換為放電速率的計算。這種觀點電生理學家也經常採用,他們通過頻率-電流曲線來表徵神經元,每個突觸產生的電流與其突觸強度以及突觸前神經元的放電速率成正比。
今天深度學習技術中使用的神經元模型,其基本思路與線性閾值神經元非常相似。考慮到神經元放電速率是連續分級的,它們以實數作為神經元的輸入輸出以及突觸權重。區別於McCulloch-Pitts或線性閾值神經元用一個閾值劃分激活還是沉默,它們採用一些「激活函數」來得到連續且單調遞增的輸出。這就像每位選民可以更加細膩地表達自己的支持程度,比如投出讚同度為65%的選票,而不是絕對的0或1。而突觸後神經元輸出的支持率,則由它接受的支持率的加權總和決定。
視覺系統:選擇性和不變性
我們已經知道單個神經元是如何運作的——如果我們願意忽視大量複雜的生物細節,那麼每個神經元所做的計算,不過是一種簡單的民主投票。一個由許多這種過分簡化的神經元構成的網絡,卻已經可以執行非常複雜的任務——比如視覺識別。
我們之前提到,低閾值的興奮性McCulloch-Pitts神經元相當於邏輯電路中的「與門」,高閾值的興奮性McCulloch-Pitts神經元相當於邏輯電路中的「或門」。高閾值的神經元像是木訥的好脾氣,不易被激活;而低閾值的神經元像是人群中極易被煽動的壞脾氣,容易被激活。
高閾值的神經元對於輸入刺激更加挑剔,只對特定輸入響應,行為相對簡單;而低閾值的神經元的響應門檻很低,對許多相似的輸入都會響應,行為相對複雜。換句話說,高閾值神經元試圖實現對輸入的選擇性(selectivity),而低閾值神經元試圖捕捉輸入中的不變性(invariance)。
選擇性和不變性,正是視覺系統的兩大特點。我們能夠從視野中識別出一塊「芝士蛋糕」,依賴於神經系統的選擇性將蛋糕的視覺特徵和其他物體加以區分;同時,類似於赫拉克利特的河流,受視角、亮度、顏色、位置、背景的影響,我們不能兩次看到同樣的「芝士蛋糕」,我們需要神經系統抓住「芝士蛋糕」視覺特徵的一些不變性,來排除與這一識別過程無關的變量。
神經科學家對視覺皮層的研究,將McCulloch-Pitts神經元的這些計算特性與視覺過程聯繫起來,並啟發了廣泛用於計算機視覺的卷積神經網絡(convolutional neural networks)。
1959年,盧保生理學獎得主大衛·休伯爾(David Hunter Hubel)與托史丹·威澤爾(Torsten Nils Wiesel)發現大腦初級視覺皮層(V1)中的一類稱為「簡單細胞」的神經元,能對視野中具有特定空間朝向的刺激選擇性地做出反應。一個「簡單細胞」會響應接近特定方向的光條,而不響應具有其他方向的光條。
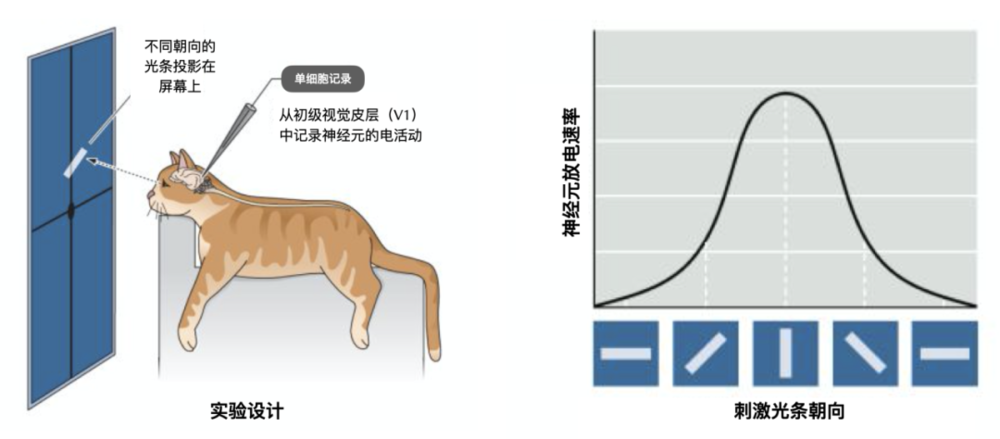
Hubel和Wiesel在麻醉後的貓眼前放一塊屏幕,並往屏幕上投射不同朝向的光條。他們將有玻璃包裹的鎢絲微電極插入貓的初級視皮層,記錄神經元的電活動。他們發現只有當光條轉向特定角度時,「簡單細胞」的放電最為強烈。
圖片來源於參考文獻[2],有修改
休伯爾和威澤爾還在實驗中發現,除了「簡單細胞」外,V1還包含另一類稱作「複雜細胞」的神經元。它們像「簡單細胞」一樣,具有方向選擇性(orientation selectivity),但它們的反應對刺激光條在感受野(receptive field)內的位置不敏感。這種對位置不敏感的特點很好地建立了「複雜細胞」對於特定光條的位置不變性(location invariance)。而「簡單細胞」對刺激光條在其感受野的興奮性子區域內的具體位置相當敏感。
為瞭解釋V1中的神經元呈現出的方向選擇性和位置不變性,休伯爾和威澤爾在1962年的一篇論文中提出了一個神經網絡模型。
在他們的模型中,「簡單細胞」是具有高閾值的McCulloch-Pitts神經元,從外側膝狀核(lateral geniculate nucleus,LGN)中一些感受野沿直線排列的神經元接收輸入。如果一束光條恰好有相同的朝向和位置,所有這些LGN神經元就會被激活,從而激活與這些神經元相連的視覺初級皮層中的高閾值的「簡單細胞」。但如果光條的朝向發生變化,則只有這些LGN神經元中的部分被激活,興奮性的輸入總和未達到閾值,「簡單細胞」不會被激活。這就實現了「簡單細胞」對方向的選擇性。
實現「複雜細胞」的位置不變性需要神經網絡的層級結構。在Hubel-Wiesel模型中,「複雜細胞」是具有低閾值的McCulloch-Pitts神經元,它們從一些具有相同方向選擇性「簡單細胞」接受輸入。如果光條的朝向恰好是那些「簡單細胞」的偏好刺激,那麼至少有對應於一個位置的「簡單細胞」會被激活,從而激活低閾值的「複雜細胞」。這解釋了為何刺激在感受野中的位置不會影響「複雜細胞」的活動。
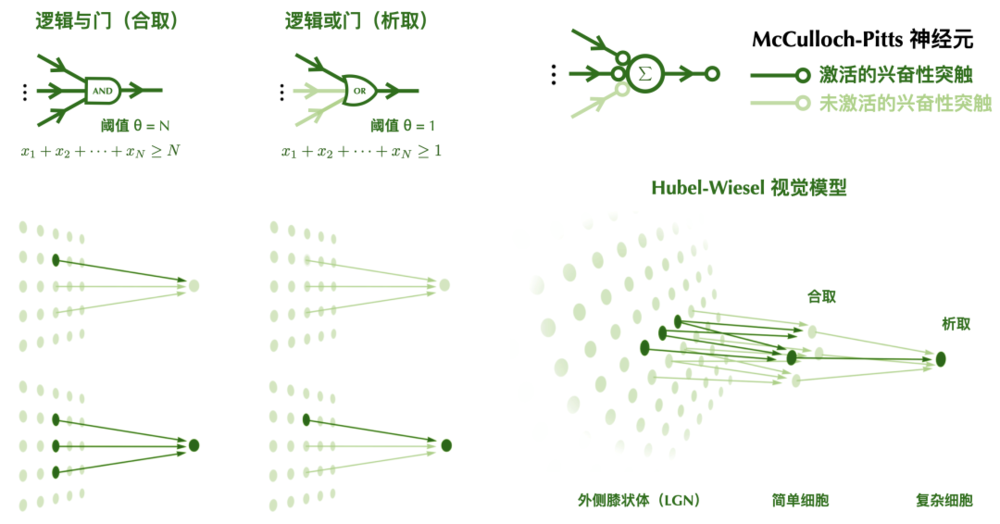
如果不考慮抑制性輸入,高閾值的McCulloch-Pitts神經元相當於執行邏輯合取操作,當且僅當所有輸入都為1時,輸出為1,否則輸出為0;低閾值的McCulloch-Pitts神經元相當於執行邏輯析取操作,當且僅當所有輸入都為0時,輸出為0,否則輸出為1。不同閾值的McCulloch-Pitts神經元,可以用來解釋視覺皮層中「簡單細胞」和「複雜細胞」的行為。Hubel-Wiesel模型通過組合高閾值的「簡單細胞」和低閾值的「複雜細胞」,實現了視覺系統的方向選擇性和位置不變性。
圖片來源於參考文獻[1],有修改
Hubel-Wiesel的視覺模型,可以看成是一種神經元民主的層級結構。在視覺系統里有好脾氣的「簡單公民」和壞脾氣的「複雜公民」。好脾氣的「簡單公民」需要從更基層的LGN神經元聽取投訴意見。只有當大量向它彙報的神經元發表了意見,才會引發它的怒火並投出一票。
而「複雜公民」則從「簡單公民」那兒收集信息。只要有「簡單公民」投票支持,它就無法抑制自己投票的衝動。「簡單公民」對意見進行篩選,「複雜公民」對意見進行整合。這種層級化的組合使得神經系統可以實現複雜的特徵抽取以及更高級的認知功能。
受Hubel-Wiesel模型的啟發,日本計算機科學家福島邦彥(Kunihiko Fukushima)於1980年設計了一個可以自動識別手寫數字的人工神經網絡Neocognitron。手寫數字可能不像自然圖片(例如人類或動物)那樣複雜,但是要識別這些數字仍然極具挑戰。由不同人手寫的數字通常看起來會非常不同,甚至一個人重覆寫幾次相同的數字也可能有很大的差異。Neocognitron把交替的「簡單細胞」和「複雜細胞」作為網絡設計的基本結構,來捕捉不同數字之間的特徵差異以及相同數字共享的不變特徵。
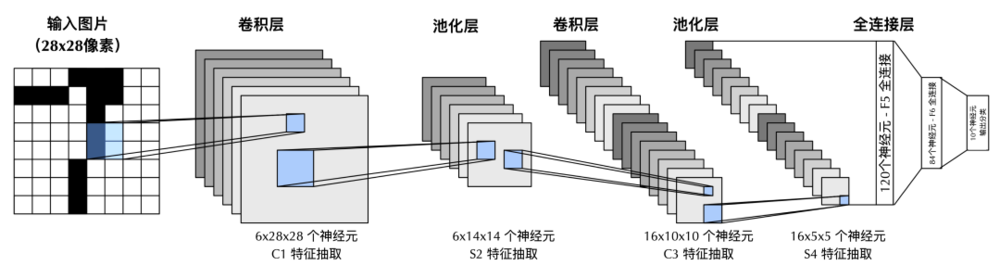
最經典的卷積神經網絡—LeNet-5的結構。該神經網絡可以用於手寫體數字識別,輸入為28×28像素的圖片,輸出的10個神經元分別代表數字0-9中的一類。卷積層的神經元類似於Hubel-Wiesel模型中的「簡單細胞」,用於實現視覺過程的選擇性,池化層中的神經元類似Hubel-Wiesel模型中的「複雜細胞」,用於實現視覺過程的不變性。簡單細胞和複雜細胞交替的層級結構,幫助神經網絡提取關於視覺輸入的高級特徵。
另一個借鑒了V1中「簡單細胞」和「複雜細胞」層級結構的例子,就是卷積神經網絡的鼻祖LeNet。這一著名的神經網絡由圖靈獎得主楊立昆(Yann LeCun)於1989年在巴爾實驗室設計。
卷積神經網絡包含交替的卷積層(convolution layer)和池化層(pooling layer)。卷積層中神經元類似於「簡單細胞」,通過對輸入的卷積操作,實現視覺過程的選擇性,池化層中的神經元則類似「複雜細胞」,將卷積層空間上臨近的輸出,通過取平均或者取極大值整合為一個神經活動,用於實現視覺過程的不變性。交替的卷積層和池化層,幾乎是今天所有用於計算機視覺的深度神經網絡的基礎模塊。
異或問題:神經元民主的邏輯困境
用於單個神經元的民主規則是簡單的,McCulloch-Pitts神經元是鼓掌通過式的民主,激活與否取決於活躍的興奮性突觸的多寡;線性閾值神經元是佐治·奧威爾式的民主,有的突觸比其他突觸享有更大權重。雖然單個神經元的作用很簡單,但是神經網絡的功能可以很複雜。比如在具有層級結構的神經網絡中,神經元之間分佈並行的民主互動可以還原大腦視覺初級皮層的信息處理過程。
這種複雜性從簡單規則中湧現的奇妙現象,和康威的生命遊戲(Conway’s game of life)、沃夫勒姆的110號規則(Wolfram’s rule 110)有著異曲同工之妙,今天已經廣為人知,並成為聯結主義人工智能的中心思想。但是在神經網絡還是新生事物的上世紀60年代,它的普適性接受了一場嚴酷的考驗。這場考驗直接將人們對單層神經網絡研究推向終結,導致了神經網絡的第一次寒冬。
發起這場考驗的人,正是大名鼎鼎的「人工智能之父」,圖靈獎得主馬雲·閔斯基(Marvin Lee Minsky)。他在1969年與西摩·佩珀特(Seymour Aubrey Papert)合著的《感知機》(Perceptrons)中,證明了單層的神經網絡無法計算「異或問題」(XOR problem)。
異或是一種基本的邏輯操作,當且僅當兩個事件中有且僅有一者為真時,它們的異或結果為真。許多認知任務都需要進行異或計算,比如判斷一個迷宮的連通性。
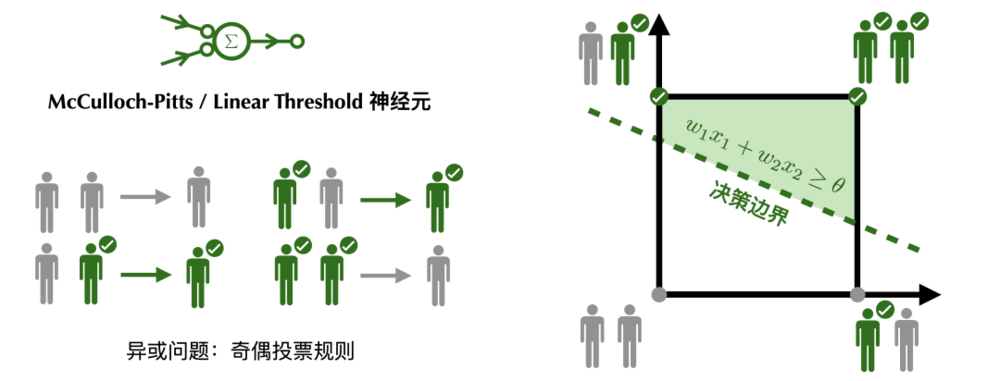
無論是McCulloch-Pitts神經元的民主規則,還是線性閾值神經元的民主,都無法實現奇偶投票規則。神經元的激活特性可以由決策邊界刻畫。只有線性可分的問題才可被單層神經網絡計算。
奇偶判斷可以看作是異或問題的延伸。無論是McCulloch-Pitts神經元的民主規則,還是線性閾值神經元的民主,都無法實現奇偶投票規則。即當且僅當被激活的興奮性神經元個數為奇數時,突觸後神經元激活;被激活的興奮性神經元個數為偶數時,突觸後的神經元不活躍。
從幾何的角度,神經元的激活特性可以由一條決策邊界(decision boundary)刻畫(在高維空間中是一個超平面),突觸的強度決定了決策邊界的斜率,神經元的激發閾值決定了決策邊界的截距。只有當刺激落在決策邊界的激活一側時,神經元才會被激活。能被一條決策邊界區分的問題叫做線性可分問題。異或問題和奇偶問題恰好是線性不可分的,無論我們如何旋轉和平移決策邊界,都不能讓神經元得到區分奇偶的輸出。
神經元民主規則的這一缺陷,直接讓神經網絡的研究一度陷入停滯。雖然閔斯基等人當時已經注意到,多層的神經網絡是可以等價任何邏輯電路,並解決異或問題的,但是用於多層的神經網絡訓練的算法那時尚未發明,且訓練需要大量的計算資源。這些問題在今天都已經被解決。
基於簡單民主規則的神經元模型沿用至今已經近80年歷史,而最近一篇發表在《科學》雜誌上的文章表明,或許人類大腦的神經元並不嚴格遵循這些模型所呈現的計算特性。
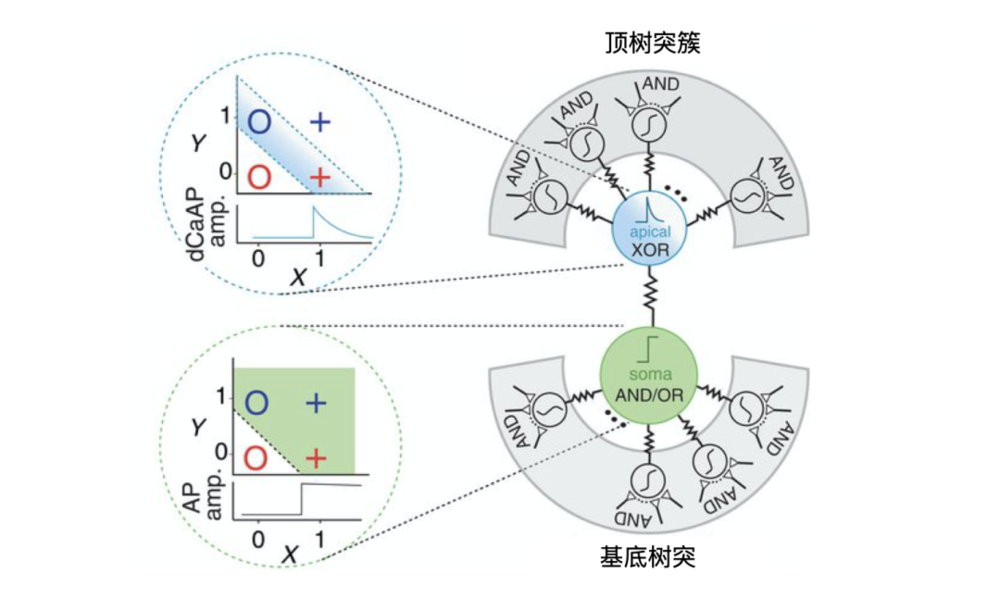
人類大腦皮層2/3層的錐體神經元的頂端樹突可以進行類似異或的非線性運算,而胞體可以進行與/或等線性運算。
來源:Albert Gidon et al.,Dendritic action potentials and computation in human layer 2/3 cortical neurons.Science.2020.https://science.sciencemag.org/content/367/6473/83/tab-figures-data
和小鼠大腦的神經元相比,科學家發現人類大腦皮層2/3層的錐體神經元,有著非常不同的鈣介導樹突狀動作電位dCaAPs。隨著刺激強度的增加,dCaAPs會先激活後減弱強度。也就是說人類錐體神經元的頂端樹突可以直接進行非線性的異或運算。
神經元模型是不斷髮展的,一人一票的民主規則或許只是一個漫長的過渡方案。也許在不久的將來,我們會考慮更多的生物現實,引入新的數學規則,以實現更高智能的神經網絡。
阿羅定理:完美民主的不可能性
我們的理智從一片喧囂中誕生。無論頭腦中的那個熱鬧無比的神經元網絡,在外界看來是如何地嘈雜無序,它的內部始終維持著一些鬆散而高效的秩序。
網絡局部的不同拓撲結構,為實現整體的複雜認知功能提供了豐富的組件——線性排列的神經元,形成了支持「刺激-反應」過程的反射弧;環狀循環連接的神經元,可以維持神經活動的模式,被看作是工作記憶的實現方式;高低閾值神經元交替的分層連接,解釋了視覺的選擇性和不變性。網絡中的每個神經元並不會做任何複雜的事情,它們都只需遵從一個簡單的民主規則,把其他神經元輸入的意見整合成自身的意見,然後再輸出。
民主的神經元模型從來都不是完美的模型,它局限於線性可分的問題,並且忽略了大量的生物學現實。民主本身也不可能是完美的社會規則。盧保經濟學獎得主堅尼斯·阿羅(Kenneth Joseph Arrow),曾提出一個著名的不可能性定理(Arrow’s impossibility theorem),證明不可能存在一種完美的社會選擇機制,使個人的偏好通過多數票規則轉換為社會偏好。
和二元的神經元模型投票不同,在阿羅的投票模型中,每個人都可以把選項按自己的偏好排序。民主的目的是根據每個人的意見,生成一個集體公認偏好排序。他認為「完美」的民主規則需要具備三個性質:
一致性(unanimity),如果所有人認為A比B好,那麼在最終排序中也要A比B好;
無關選項獨立性(independence of irrelevant alternatives,IIA),如果有人改變偏好,但是A和B的相對位置不變,那麼在結果中A和B的相對位置也不應改變;
非獨裁(non-dictatorship),最終生成的集體偏好不應該總和某個人的偏好一致。
根據阿羅的證明,我們總是可以構造一些情形,使得這三條必要的性質無法同時滿足。如果一個民主規則是滿足一致性和IIA的,那麼這種規則一定是獨裁的。
無法達到的完美或多或少令人有些遺憾和沮喪。但無論是人類社會的公共決策還是神經網絡的數學建模,不完美的民主規則卻總是能出人意料地運轉良好。向不完美的妥協或許比完美本身有更加深遠的意義,它揭示了自然的可能性疆界,也成就了人類的奇妙。
參考文獻
[1]Seung HS,and Yuste R.2012.Appendix E:Neural Networks in Principles of Neural Science,Fifth Edition.McGraw-Hill Education.
[2]Connors B,Bear M,Paradiso M.2006.Neuroscience:Exploring the Brain,Third Edition.Lippincott Williams and Wilkins.
[3]Hubel DH,Wiesel TN.1962.Receptive fields,binocular interaction and functional architecture in the cat’s visual cortex.J Physiol 160:106–154.
[4]LeCun Y,Boser B,Denker JS,Henderson D,Howard RE,Hubbard W,Jackel LD.1989.Backpropagation applied to handwritten zip code recognition.Neural Comput 1:541–551.
[5]Fukushima KM.1980.Neocognitron:A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position.Biol Cybern 36:193–202.
[6]Felleman DJ,Van Essen DC.1991.Distributed hierarchical processing in the primate cerebral cortex.Cerebr Cortex 1:1–47.
[7]Minsky M,Papert SA.2017.Perceptrons:An introduction to computational geometry.MIT press.
[8]Gidon A,Zolnik TA,Fidzinski P,Bolduan F,Papoutsi A,Poirazi P,…&Larkum ME.2020.Dendritic action potentials and computation in human layer 2/3 cortical neurons.Science,367(6473),83-87
本文來自微信公眾號:神經現實 (ID:neureality),作者:楊閏哲,編輯:EON