AI「長腦子」了？LLM驚現「人類腦葉」結構並有數學代碼分區，MIT大牛新作震驚學界！

新智元報導  

編輯：編輯部 HYZ

【新智元導讀】Max Tegmark團隊又出神作了！他們發現，LLM中居然存在人類大腦結構一樣的腦葉分區，分為數學/代碼、短文本、長篇科學論文等部分。這項重磅的研究揭示了：大腦構造並非人類獨有，矽基生命也從屬這一法則。

LLM居然長「腦子」了？

就在剛剛，MIT傳奇大牛Max Tegmark團隊的新作，再次炸翻AI圈。

他們發現，LLM學習的概念中，居然顯示出令人驚訝的幾何結構——

首先，它們形成一種類似人類大腦的「腦葉」；其次，它們形成了一種「語義晶體」，比初看起來更精確；並且，LLM的概念雲更具分形特徵，而非圓形。

具體而言，這篇論文探討了LLM中稀疏自編碼器（SAE）的特徵向量表示的。

Max Tegmark團隊的研究結果表明，SAE特徵所代表的概念宇宙在多個空間尺度上展現出有趣的結構，從語義關係的原子層面到整個特徵空間的大規模組織。

這就為我們理解LLM的內部表徵和處理機制，提供了全新的見解。

總之，這個研究實在太過震撼！網民直言：如果LLM和人腦相似，這實在是給人一種不好的預感……

所以，美麗的自然法則並不獨屬於人類，矽基也從屬於這一法則。

這個發現證明了：數學才是一切的基礎，而非人類構造。

LLM的三個層面：原子，大腦和星系

團隊發現，SAE特徵的概念宇宙在三個層面上都具有有趣的結構：

小尺度「原子」

中尺度「大腦」

大尺度「星系」

原子級的微觀結構，包含面為平行四邊形或梯形的「晶體」，這是對經典案例的推廣（比如「男人-女人-國王-王后」的關係）。

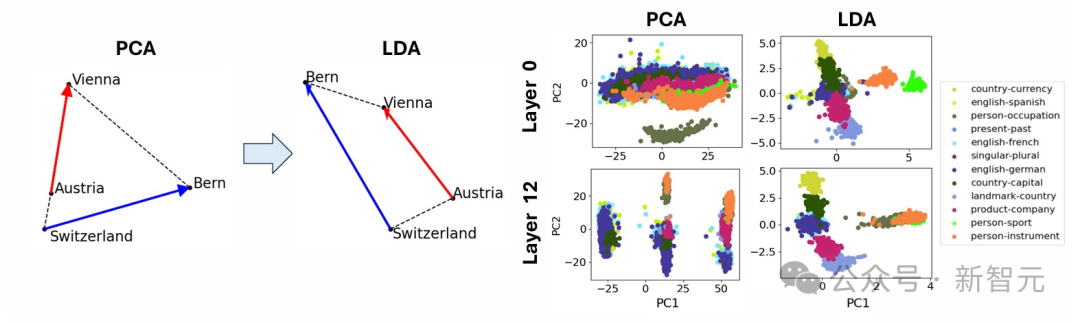
他們發現，當使用線性判別分析（LDA）高效地投影出諸如詞長等全局干擾方向時，這些平行四邊形和相關函數向量的質量會顯著提升。

而類似「大腦」的中間尺度結構，則展現出了明顯的空間模塊化特徵，團隊將其描述為空間集群和共現集群之間的對齊。

比如，數學和代碼特徵形成了一個「腦葉」，跟神經功能磁共振圖像中觀察到的人類大腦功能分區相似。

團隊運用多個指標，對這些功能區的空間局部性進行了量化分析，發現在足夠粗略的尺度上，共同出現的特徵簇在空間上的聚集程度遠超過特徵幾何隨機分佈情況下的預期值。

而在「星系」的大尺度結構上，特徵點雲並非呈各向同性（各個方向性質相同），而是表現出特徵值冪律分佈，中間層的斜率最抖。

而聚類熵也在中間層周圍達到峰值！

看完這個研究，有網民給出了這樣的評價——

「如果這項研究出自Max Tegmark之外的任何人，我都會覺得他是瘋子。但Tegmark是我們這個時代最優秀的科學家之一。當我說意識是一種數學模式、一種物質狀態時，我引用的是他。」

LLM學習概念中，驚人的三層幾何結構

去年，AI圈在理解LLM如何工作上取得了突破，稀疏自編碼器在其激活空間中，發現了大量可以解釋為概念的點（「特徵」）。

稀疏自編碼器作為在無監督情況下發現可解釋語言模型特徵的方法，受到了很多關注，而檢查SAE特徵結構的工作則較少。

這類SAE點雲最近已經公開，MIT團隊認為，是時候研究它們在不同尺度上的結構了。

「原子」尺度：晶體結構

在SAE特徵的點雲中，研究者試圖尋找一種稱之為「晶體結構」的東西。

這是指反映概念之間語義關係的幾何結構，一個經典的例子就是（a, b, c, d）=（男人，女人，國王，女王）。

它們形成了一個近似的平行四邊形，其中b−a≈d−c。

這可以解釋為，兩個函數向量b−a和c−a分別將男性實體變為女性，將實體變為皇室。

研究者還搜索了只有一對平行邊b−a ∝ d−c的梯形（對應於僅一個函數向量）。

圖1（右）即為這樣的一個例子：（a, b, c, d）=（奧地利，維也納，瑞士，伯爾尼），其中函數向量可以解釋為將國家映射到其首都。

研究者通過計算所有成對的差向量並對其進行聚類來搜索晶體，這應該會產生與每個函數向量相對應的一個簇。

簇中的任何一對差向量，應該構成梯形或平行四邊形，這取決於在聚類之前差向量是否被歸一化（或者可以等效於，是否通過歐幾里得距離或餘弦相似度，來量化了兩個差向量之間的相似性）。

最初搜索SAE晶體時，研究者發現的大多是噪聲。

為什麼會出現這種情況？

為了調查原因，研究者將注意力集中在了在第0層（token嵌入）和第1層，在這些層中，許多SAE特徵與單個詞相對應。

然後，他們研究了Gemma2 2B模型中來自數據集的殘差流激活，這些激活對應於先前報告的詞->詞函數向量，於是搞明白了這個問題。

這與多篇論文指出的情況一致，即（男，女，國王，王后）並不是一個準確的平行四邊形。

之所以會有這種現象，是因為存在一種所謂的「干擾特徵」。

比如，圖1（右）中的橫軸主要對應於單詞長度。

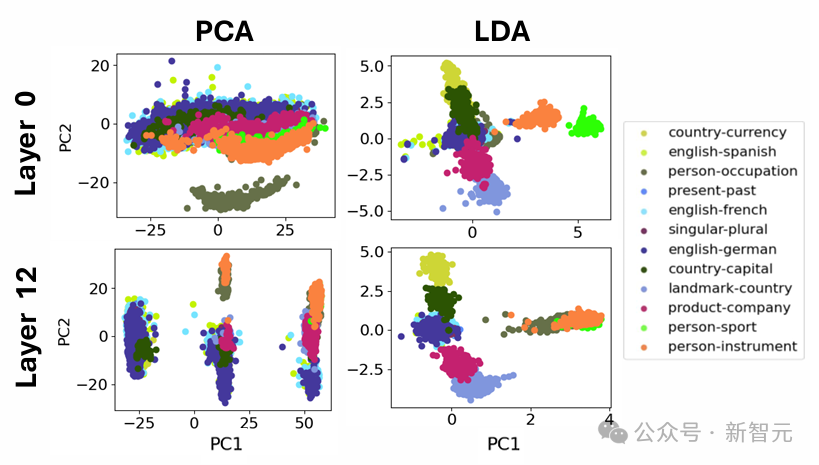
這在語義上是不相關的，並且對梯形（左）造成了嚴重破壞，因為「Switzerland」要比其他的詞長很多。

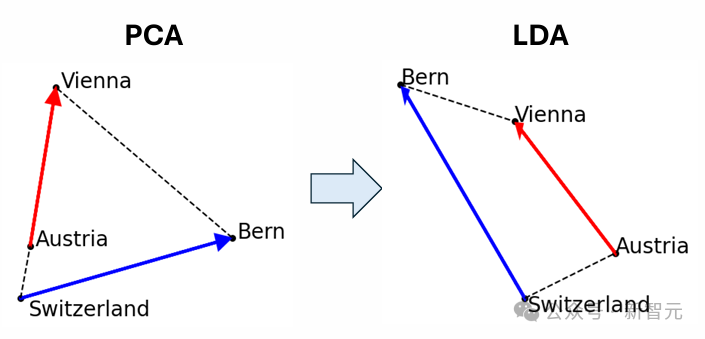
為了消除這些語義上無關的干擾向量，研究者希望將數據投影到與這些干擾向量正交的低維子空間上。

對於數據集，他們使用了線性判別分析（LDA）來實現這一點。LDA將數據投影到信號噪聲比特徵模式上，其中「信號」和「噪聲」分別定義為簇間變化和簇內變化的協方差矩陣。

這種彷彿顯著改善了簇和梯形/平行四邊形的質量，突顯出干擾特徵可能掩蓋了現有的晶體結構。

「大腦」尺度：中等尺度的模塊結構

接下來，我們到了論文最精彩的地方。

在這一部分，研究者們縮小了視角，試圖尋找更大規模的結構。

他們研究了功能相似的SAE特徵組（這些特徵組傾向於一起激活），想看看它們是否在幾何上也是相似的，是否會在激活空間中形成「腦葉」。

在動物的大腦中，這種功能組就是眾所周知的神經元所在的三維空間中的簇。

例如，布羅卡區涉及語言生成，聽覺皮層處理聲音，杏仁核主要處理情緒。

研究者非常好奇，是否可以在SAE特徵空間中找到類似的功能模塊呢？

他們測試了多種方法，來自動發現這類功能性「腦葉」，並量化它們是否是空間模塊化的。

他們將腦葉分區定義為點雲的一個k子集的劃分，這種分區的計算不使用位置信息，相反，他們是基於它們在功能上的關聯性來識別這些腦葉分區的。

具體來說，這些腦葉在同一文檔內傾向於一起激活。

為了自動識別功能腦葉，研究者首先計算了SAE特徵共現的直方圖。

他們使用Gemma2 2B模型處理了來自The Pile的文檔。

研究者發現，在第12層的殘差流SAE具有16k個特徵，平均L0為41。

他們記錄了這個SAE被激活的特徵（如果某特徵的隱藏激活值> 1，則將其視為被激活）。

如果兩個特徵在同一個256個token的塊內同時激活，則它們被視為共現。

此長度提供了一種粗略的「時間解像度」，使他們能夠發現傾向於在同一文檔中共同激活的token，而不僅限於同一token。

研究者使用了最大長度為1024的上下文，並且每個文檔只使用一個這樣的上下文，這就使他們在The Pile的每個文檔中最多有4個塊（和直方圖更新）。

他們在5萬個文檔中計算了直方圖。

基於此直方圖，他們根據SAE特徵的共現統計，計算了每對特徵之間的親和分數，並對得到的親和矩陣進行了譜聚類。

研究者嘗試了以下基於共現的親和度計算方法：簡單匹配係數、Jaccard相似度、Dice係數、重疊係數和Phi係數，這些都可以僅通過共現直方圖計算得出。

研究者們原本假設，功能上相似的點（即常見的共現SAE特徵）在激活空間中應該是均勻分佈的，不會表現出空間模塊性。

然而，出乎他們意料，圖2顯示出：腦葉在視覺上呈現出相當集中的空間分佈！

在SAE點雲中識別出的特徵傾向於在文檔中一起激活，同時也在幾何上共同定位於功能「腦葉」中，左側的2腦葉劃分將點雲大致分為兩部分，分別在代碼/數學文檔和英文文檔上激活。右側的3腦葉劃分主要將英文腦葉細分為一個包含簡短消息和對話的部分，以及一個主要包含長篇科學論文的部分

為了量化其統計顯著性，研究者使用了兩種方法來排除原假設：

1. 雖然可以基於特徵是否同時出現進行聚類，但也可以基於SAE特徵解碼向量的餘弦相似度來進行譜聚類。

他們首先使用了餘弦相似度對SAE特徵進行聚類，然後使用共現對特徵進行聚類，之後計算這兩組標籤之間的相互信息。

在某種意義上，這直接衡量了通過瞭解功能結構可以獲得多少關於幾何結構的信息。

2. 另一個方法就是訓練模型，通過幾何信息預測特徵所屬的功能腦葉。

為此，研究者將基於共現聚類得到的腦葉標籤集作為目標，使用邏輯回歸模型直接根據點的位置預測這些標籤，並使用80-20的訓練-測試集劃分，報告該分類器的平衡測試準確率。

左上：空間聚類與功能聚類之間的調整互信息。右上：邏輯回歸的平衡測試準確率，用位置預測基於共現的聚類標籤。左下：隨機置換餘弦相似度聚類標籤後的調整互信息。右下：隨機單位範數特徵向量的平衡測試準確率。報告的統計顯著性基於Phi係數的腦葉聚類

圖3顯示，對於兩種度量方法，Phi係數效果最佳，提供了功能腦葉與特徵幾何形狀之間的最佳對應關係。

為了證明其統計顯著性，研究者隨機打亂了基於餘弦相似度聚類的簇標籤，並測量了調整後的相互信息。

同時，他們使用隨機高斯分佈，對SAE特徵解碼方向重新初始化並歸一化，然後訓練邏輯回歸模型從這些特徵方向預測功能腦葉。

圖3（下）顯示，兩項測試都以極高的顯著性排除了零假設，分別達到了954和74個標準差，這就明確表明：研究者所觀察到的腦葉是真實的，而非統計偶然！

為了評估每個腦葉的專長，他們將The Pile數據集中的1萬份文檔輸入了Gemma2 2B模型，並再次記錄了第12層中每256個token塊內觸發的SAE特徵。

對於每個token塊，他們都記錄了具有最高特徵觸發比例的腦葉。

The Pile中的每個文檔都帶有名稱，指定該文檔屬於語料庫的哪個子集。對於每種文檔類型，針對該類型文檔中每個256 token塊，他們都會記錄哪一個腦葉具有最高的SAE特徵觸發比例。

跨越數千份文檔後，可以查看每種文檔類型中，哪個腦葉的激活比例最高的直方圖。

在圖4中，研究者展示了使用Phi係數作為共現度量計算的三個腦葉結果，這構成了圖2中腦葉標記的基礎。

每個腦葉都具有最高比例的激活特徵上下文分數。腦葉2通常在代碼和數學文檔上不成比例地被激活，腦葉0在包含文本（聊天記錄、會議記錄）的文檔上激活更多，腦葉1在科學論文上激活更多

圖5對比了五種不同共現度量的效果。儘管Phi係數最佳，但五種度量方法均能夠識別出「代碼/數學腦葉」。

「星系」尺度：「大規模」點雲結構

最後一種，讓我們進一步拉遠視角，看看大模型在「星系」尺度結構中，點雲的樣子。

主要是研究其整體形狀、聚類，類似於天文學家研究硬核系形狀和子結構的方式。

接下來，研究人員試圖去排除一個簡單的零假設（null hypothesis）：點雲只是從各向同性多元高斯分佈中采樣的。

如圖6直觀地表明，即使在其前三個主要成分中，點雲分佈也不完全是圓形的，某些主軸略寬於其他軸，類似人腦的形狀。

形狀分析

圖7（左）通過點雲協方差矩陣的特徵值排序，來量化這一現象。

它揭示出，這些特徵值並非是恒定的，而是呈現出冪律衰減。

為了檢驗這個令人驚訝的冪律是否顯著，圖中將其與從各向同性高斯分佈中抽取的點雲的相應特徵值譜進行比較。

結果顯示，後者更加平攤，並且與分析預測一致：

從多元高斯分佈中抽取的N個隨機向量的協方差矩陣遵循Wishart分佈

這一點，已經在隨機矩陣理論中，得到了充分的研究。

由於，最小特徵值的急劇下降是由有限數據引起的，並在N趨於無窮大時消失，研究人員在後續分析中，將點雲降維到其100個主成分。

換句話說，點雲的形狀像一個「分形黃瓜」，其在連續維度上的寬度像冪律一樣下降。

研究人員發現，與SAE特徵相比，激活值的冪律特徵明顯較弱。未來，進一步研究其成因，也將是一個有趣的方向。

圖7（右）顯示了，上述冪律的斜率如何隨LLM層數變化，這是通過對100個最大特徵進行線性回歸計算得到的。

研究人員觀察到一個清晰的模式：

中間層具有最陡的冪律斜率（第12層的斜率為-0.47），而早期和後期層（如第0層和第24層）的斜率較為平緩（分別為-0.24和-0.25）。

這可能暗示了，中間層充當了一個瓶頸，將信息壓縮到更少的主成分中，或許是為了更有效表示高層抽像概念。

圖7（右）還在對數尺度上，展示了有效雲體積（協方差矩陣的行列式）如何隨層數變化。

聚類分析

一般來說，星系或微觀粒子的聚類，通常通過冪譜或相關函數來量化。

對於研究中高維數據來說，這種量化變得很複雜。

因為底層密度會隨著半徑變化，而對於高維高斯分佈，密度強烈集中在相對較薄的球殼周圍。

由此，研究人員選擇通過估計點雲，假定采樣的分佈的「熵」來量化聚類。

他們使用k-NN方法來估計熵H，計算如下：

其中ri是點i到第k個最近鄰的距離，d是點雲的維度；n是點的數量；

常數Ψ是k-NN估計中的digamma項。作為基線，高斯熵代表了給定協方差矩陣的最大可能熵。

對於具有相同協方差矩陣的高斯分佈，熵的計算方法如下：

其中λi是協方差矩陣的特徵值。

研究人員定義聚類熵，或「負熵」，為Hgauss − H，即熵比其最大允許值低多少。

圖8顯示了不同層的估計聚類熵。可以看到，SAE點雲在中間層強烈聚集。

在未來研究中，研究這些變化是否主要取決於不同層中晶體或葉狀結構的顯著性，或者是否有完全不同的起源，將會是一個有趣的方向。

破解LLM運作機制黑箱，人類再近一步

總而言之，MIT團隊這項最新研究中，揭示了SAE點雲概念空間具有三層有趣的結構：

原子尺度的晶體結構；大腦尺度的模塊結構；星系尺度的點雲結構。

正如網民所言，親眼目睹了人類矽基孩子在我面前成長，既令人敬畏又令人恐懼。

Max Tegmark出品，必屬精品。

此前就有人發現，僅在下一個token預測上訓練的序列模型中，存在線性表徵的類似證據。

23年2月，哈佛、MIT的研究人員發表了一項新研究Othello-GPT，在簡單的棋盤遊戲中驗證了內部表徵的有效性。

在沒有任何奧賽羅規則先驗知識的情況下，研究人員發現模型能夠以非常高的準確率預測出合法的移動操作，捕捉棋盤的狀態。他們認為語言模型的內部確實建立了一個世界模型，而不只是單純的記憶或是統計，不過其能力來源還不清楚。

吳恩達對該研究表示了高度認可。

總之，這項研究在LLM中發現了「經度神經元」，在學界引起了巨大反響。

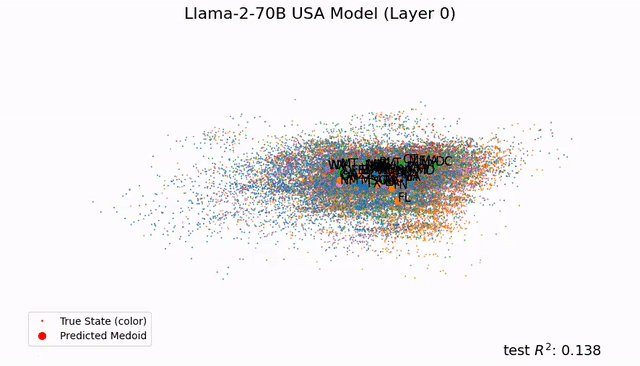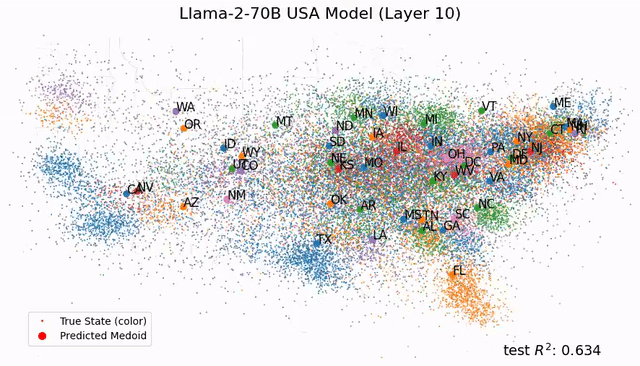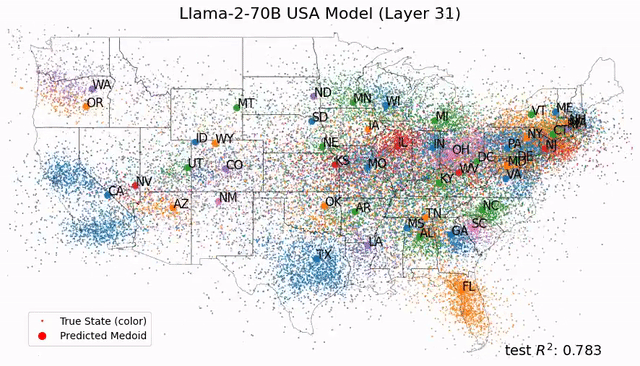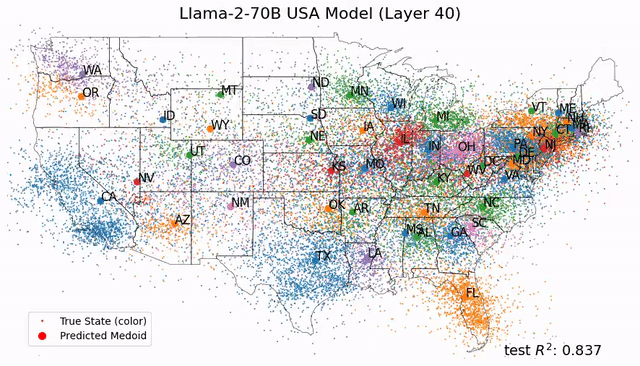
如今，Tegmark團隊又再進一步，幫我們從更微觀的角度剖析LLM的大腦。人類離解釋LLM運作機制的黑箱，又近了一步。

參考資料：

https://arxiv.org/abs/2410.19750