強化學習之父Richard Sutton給出一個簡單思路，大幅增強所有RL算法

機器之心報導

編輯：panda

在獎勵中減去平均獎勵

在當今的大模型時代，以 RLHF 為代表的強化學習方法具有無可替代的重要性，甚至成為了 OpenAI ο1 等模型實現強大推理能力的關鍵。

但這些強化學習方法仍有改進空間。近日，強化學習之父、阿爾伯塔大學教授 Richard Sutton 的團隊低調更新了一篇論文，其中提出了一種新的通用思想 Reward Centering，並稱該思想適用於幾乎所有強化學習算法。這裏我們將其譯為「獎勵聚中」。

該論文是首屆強化學習會議（RLC 2024）的入選論文之一。一作 Abhishek Naik 剛剛從阿爾伯塔大學獲得博士學位，他是 Sutton 教授的第 12 位博士畢業生。

下面我們簡要看看 Reward Centering 有何創新之處。

論文標題：Reward Centering
論文地址：https://arxiv.org/pdf/2405.09999

獎勵聚中理論

智能體和環境之間的交互可以表述為一個有限馬爾可夫決策過程（MDP）(S, A, R, p)，其中 S 表示狀態集，A 表示動作集，R 表示獎勵集，p : S × R × S × A → [0, 1] 表示轉換的動態。在時間步驟 t，智能體處於狀態 S_t，使用行為策略 b : A × S → [0, 1] 採取行動 A_t，然後根據轉換動態:

觀察下一個狀態 S_{t+1} 和獎勵 R_{t+1}。

這裏研究的問題是持續性問題，即智能體和環境的交互會無限地進行。智能體的目標是最大化長期獲得的平均獎勵。為此，該團隊考慮了估計每個狀態的預期折扣獎勵總和的方法：

這裏，折扣因子不是問題的一部分，而是一個算法參數。

獎勵聚中思想很簡單：從獎勵中減去實際觀察到的獎勵的平均值。這樣做會讓修改後的獎勵看起來以均值為中心。

這種以均值為中心的獎勵在 bandit 設置中很常見。舉個例子，Sutton 和 Barto 在 2018 年的一篇論文中表明，根據觀察到的獎勵估計和減去平均獎勵可以顯著提高學習速度。

而這裏，該團隊證明所有強化學習算法都能享受到這種好處，並且當折現因子 γ 接近 1 時，好處會更大。

獎勵聚中之所以這麼好，一個底層原因可通過折現價值函數的羅朗級數（Laurent Series）分解來揭示。

折現價值函數可被分解成兩部分。其中一部分是一個常數，並不依賴狀態或動作，因此並不參與動作選取。

用數學表示的話，對於與折現因子 γ 對應的策略 π 的表格折現價值函數

其中 r(π) 是策略 π 獲得的獨立於狀態的平均獎勵，

是狀態 s 的微分值。它們各自對於遍曆 MDP 的定義為：

則是一個誤差項，當折現因子變為 1 時變為零。狀態值的這種分解也意味著狀態-動作值有類似的分解。

這種 Laurent 級數分解能解釋獎勵聚中為何有助於解決 bandit 問題。

在完整的強化學習問題中，與狀態無關的偏移可能會相當大。舉個例子，圖 2 中展示的三狀態馬高夫獎勵過程。如果狀態從 A 變成 B，則獎勵是 +3，否則都是 0。平均獎勵為 r(π) = 1。右側表中給出了三個折現因子的折現狀態值。

現在，從每個狀態中減去常數偏移的折現值

，也被稱為聚中折現值。

可以看到，這個已經聚中的值在幅度上要小得多，並且當折現因子增大時，也只會發生輕微變化。這裏還給出了微分值以供參考。

這些趨勢普遍成立：對於任意問題，折現值的幅度都會隨著折現因子接近 1 而急劇增加，而聚中折現值則變化不大，並接近微分值。

從數學上看，聚中折現值是平均聚中獎勵的預期折現和：

其中 γ ∈ [0, 1]。當 γ = 1 時，聚中折現值與微分值相同。更一般地說，聚中折現值是微分值加上來自羅朗級數分解的誤差項，如上圖右側所示。

因此，獎勵聚中能夠通過兩個組件（恒定平均獎勵和聚中折現值函數）捕獲折現值函數中的所有信息。這種分解非常有價值：

當γ→1時，折現值趨於爆炸，但聚中折現值仍然很小且易於處理。
如果問題的獎勵偏移了一個常數 c，那麼折現值的幅度就會增加 c/(1 − γ)，但聚中折現值會保持不變，因為平均獎勵也會增加 c。

使用獎勵聚中時，還可以設計出在智能體的生命週期內可以改變折現因子（算法參數）的算法。對於標準折現算法來說，這通常是低效或無效的，因為它們的非聚中值可能會發生巨大變化。相比之下，聚中值可能變化不大，當折現因子接近 1 時，變化會變得微不足道。

當然，為了獲得這些潛在好處，首先需要基於數據估計出平均獎勵。

簡單獎勵聚中以及基於價值的獎勵聚中

估計平均獎勵最簡單的方法是根據之前已經觀察到的獎勵估計平均值。也就是說，如果

。更一般地，可以使用步長參數 βt 來更新該估計：

表示 t 個時間步驟後的平均獎勵估計，則

該團隊表示，這種簡單的聚中方法適用於幾乎任何強化學習算法。舉個例子，獎勵聚中可以與傳統的時間差分（TD）學習組合起來學習一個狀態-價值函數估計：

此外，他們還提出了基於價值的獎勵聚中。這種方法的靈感來自強化學習的平均獎勵公式。Wan et al. (2021) 表明，使用時間差分（TD）誤差（而不是 (4) 中的傳統誤差）可以對錶格離策略設置中的獎勵率進行無偏估計。事實證明，平均獎勵公式中的這個思路在折扣獎勵公式中也非常有效。

該團隊表明，如果行為策略採取目標策略所做的所有操作，那麼可以使用 TD 誤差很好地近似目標策略的平均獎勵：

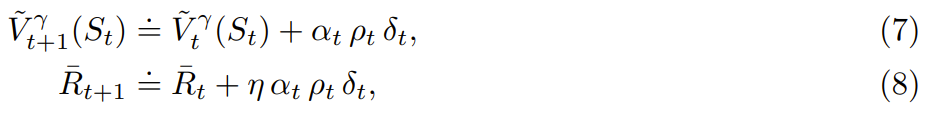
由於這種聚中方法除了獎勵之外還涉及價值，因此他們將其稱為基於價值的聚中。不同於簡單的獎勵聚中，現在平均獎勵估計和價值估計的收斂是相互依賴的。

實驗

該團隊實驗了 (5) 式的四種算法變體版本，並測試了不同的折現因子。詳細過程請閱讀原論文，這裏我們簡單看看結果。

如圖 3 所示，當獎勵由一個 oracle 進行聚中處理時，學習曲線的起點會低得多。對於其它算法，第一個誤差都在 r(π)/(1 − γ) 量級。

無聚中的 TD 學習（藍色）最終達到了與 oracle 聚中算法（橙色）相同的誤差率，這符合預期。

簡單聚中方法（綠色）確實有助於更快地降低 RMSVE，但其最終誤差率會稍微高一點。這也符合預期，因為平均獎勵估計會隨時間而變化，導致與非聚中或 oracle 聚中版本相比，更新的變數更大。當 γ 更大時也有類似的趨勢。這些實驗表明，簡單的獎勵聚中技術在在策略設置中非常有效，並且對於較大的折扣因子，效果更為明顯。

在學習率和漸近誤差方面，基於價值的獎勵聚中（紅色）在在策略問題上與簡單聚中差不多。但在離策略問題上，基於價值的聚中能以更快的速度得到更低的 RMSVE，同時最終誤差率也差不多。

總體而言，可以觀察到獎勵聚中可以提高折現獎勵預測算法（如 TD 學習）的學習率，尤其是對於較大的折扣因子。雖然簡單獎勵聚中方法已經相當有效，但基於價值的獎勵聚中更適合一般的離策略問題。

此外，該團隊還研究了獎勵聚中對 Q 學習的影響。具體的理論描述和實驗過程請訪問原論文。