o1不是唯一路徑!MIT新研究:在測試時訓練,模型推理能力最高昇至5.8倍
基爾西 發自 凹非寺
量子位 | 公眾號 QbitAI
o1不是通向大模型推理的唯一路徑!
MIT的新研究發現,在測試時對大模型進行訓練,可以讓推理水平大幅提升。
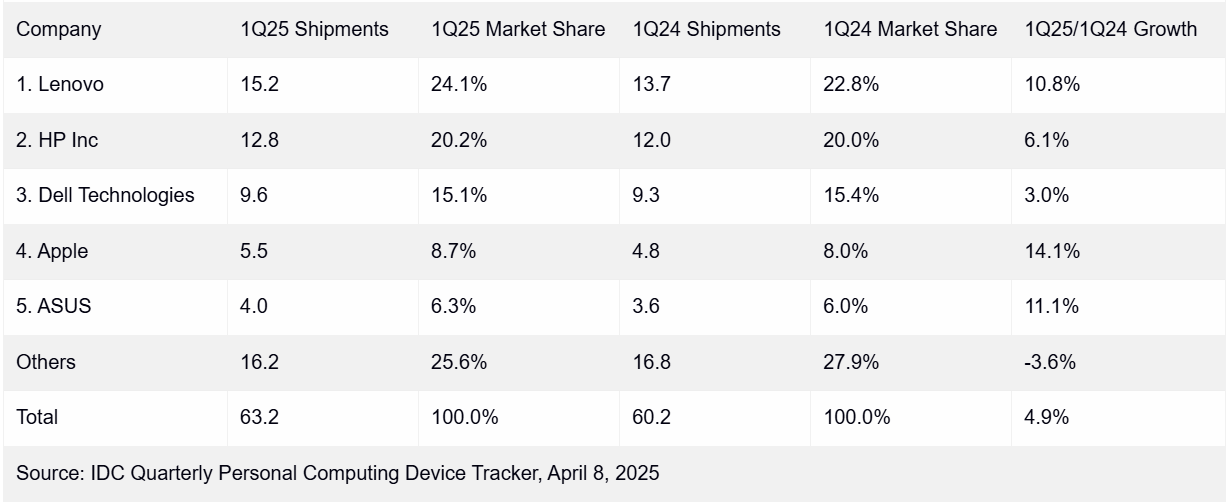
在挑戰超難的ARC任務時,準確率最高可提升至原來的5.83倍。
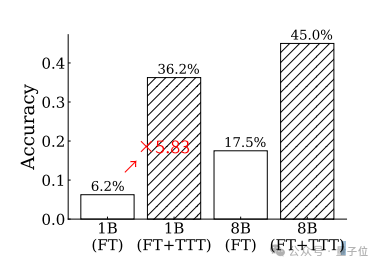
這樣的表現不僅優於GPT-4和Claude,如果與其他推理方法相結合,還能超越人類的平均水準。
OpenAI o1團隊成員Noam Brown表示,o1的大規模計算可能不是最好的方法,很高興看到有學者在提高推理能力上探索新的方法。

在測試中訓練模型
不同於傳統的先訓練後測試模式,測試時訓練(Test-Time Training,湯臣T)在部署階段面對新的測試樣本時,不直接用訓練好的模型去推理。
在推理之前,測試樣本自身攜帶的信息,會通過快速的訓練過程被用於調整模型參數。
總體來說,湯臣T過程中一共有三個關鍵階段——訓練數據生成、模型適應範式設計以及推理階段的策略。
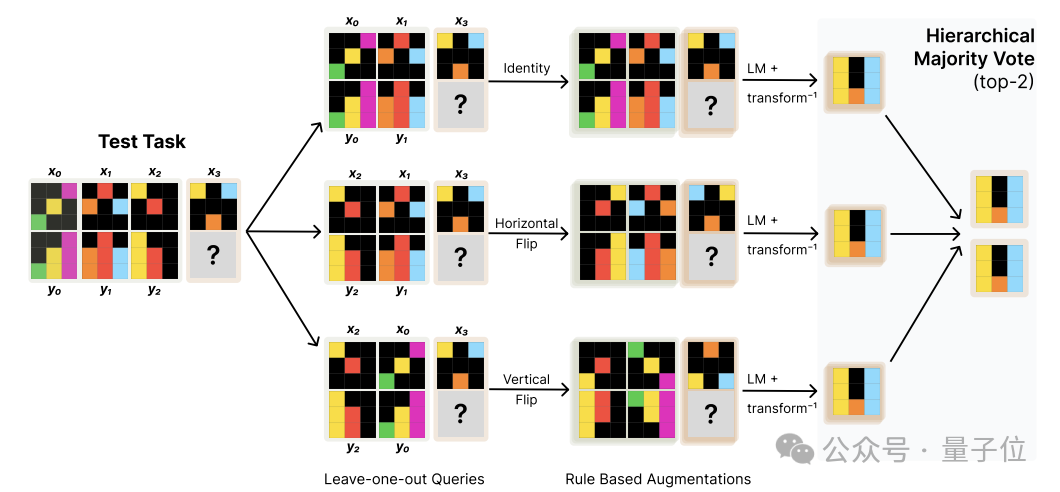
數據生成的核心是將測試任務中蘊含的輸入輸出對關係,通過數據增強的方式最大限度地利用,可具體分為兩個步驟。
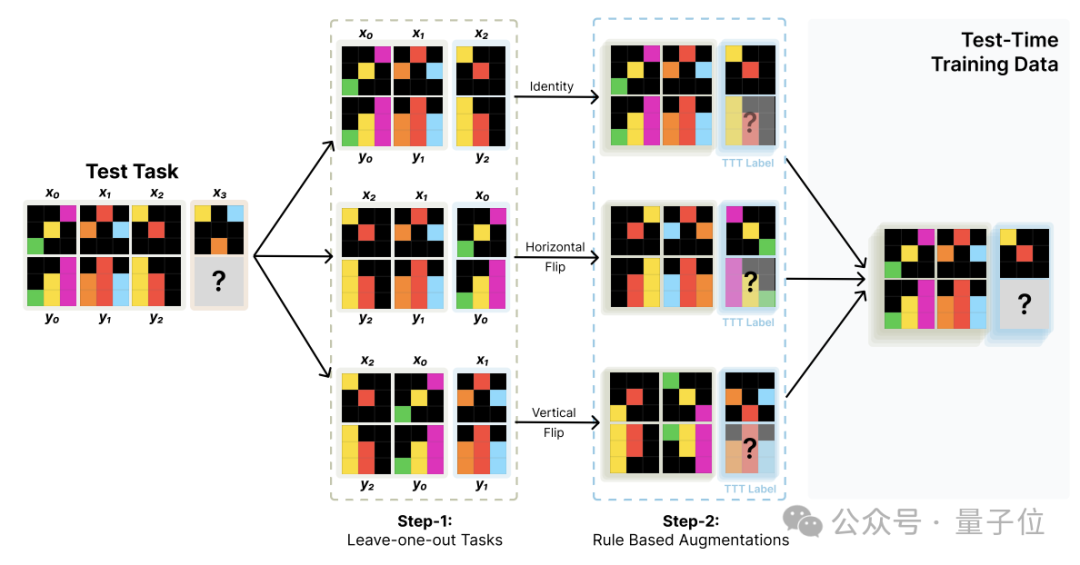
首先是基於leave-one-out構造新的任務。
對於包含K個輸入輸出對的測試任務,依次將每個樣本留出作為測試樣本,其餘K-1個作為訓練樣本,由此構造出K個新的湯臣T訓練任務。
這樣就可以從一個測試任務出發,構造出K個結構一致但內容互補的新任務,從而擴充了湯臣T訓練數據。
在此基礎上,作者還進行了數據增強,主要包括對輸入輸出施加各類幾何變換,以及打亂訓練樣本對的順序。
經過這一步,湯臣T訓練集的規模可以得到顯著擴大。
整個湯臣T數據構造過程可高度自動化,不依賴人工標註。
利用構造好的湯臣T數據集,就可以對預訓練好的語言模型進行測試時訓練。
考慮到測試時的資源限制,作者採用了參數高效的LoRA,為每個測試任務學習一組獨立的adapter參數,附加在預訓練模型的每一層之上,通過一個低秩矩陣與原始權重相乘起到調節作用。
過程中還額外加入了對所有前綴序列的預測,目的是通過在各種長度的演示樣本上都計算損失,鼓勵模型儘早地從少量信息中總結出抽像規律,從而提高魯棒性。

最後,為了實現湯臣T效果的最大化,作者在推理階段應用了數據增強和集成學習策略。
推理過程中,先利用一系列預定義的幾何變換算子(如旋轉、翻轉等)擴充原始輸入,生成若乾等價視角下的輸入變體。
之後將每個變體輸入並行地送入LoRA-tuned模型,獨立完成預測,然後再對齊和還原到原始輸入空間,由此得到一組成對的預測。
在成對預測的基礎上,通過分兩層投票的方式完成集成融合:
-
第一層在每種變換內部進行投票,選出置信度最高的Top-3個預測;
-
第二層在不同變換的Top-3預測之間進行全局投票,選出最終的Top-2作為輸出。
這一推理策略,既通過數據增強引入了輸入的多樣性,又用分層投票的方式對不同來源的預測進行了結構化的組合,進一步提升了湯臣T方法的效果。
ARC任務準確率最高昇至6倍
為了評估湯臣T方法的效果,研究團隊以8B參數的GPT-3作為基礎模型進行了測試。
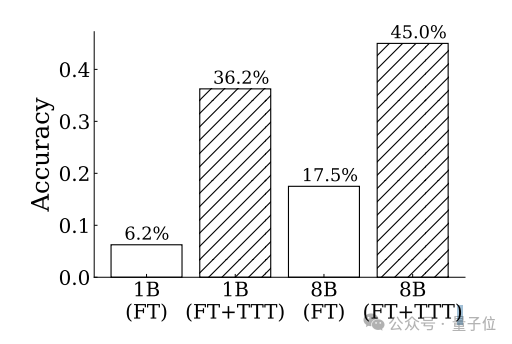
如果不使用湯臣T僅進行微調,模型在ARC數據集上的準確率只有18.3%,加入湯臣T後提升到47.1%,增長率達到了157%。

另外,作者還從ARC數據集中隨機選擇了80個任務作為子集進行了測試。
測試發現,湯臣T方法對於1B模型的提升效果更加明顯,調整後模型的準確率接近調整前的6倍。
並且在調整前後,1B和8B兩個規模的模型之間的相對差距也在縮小。
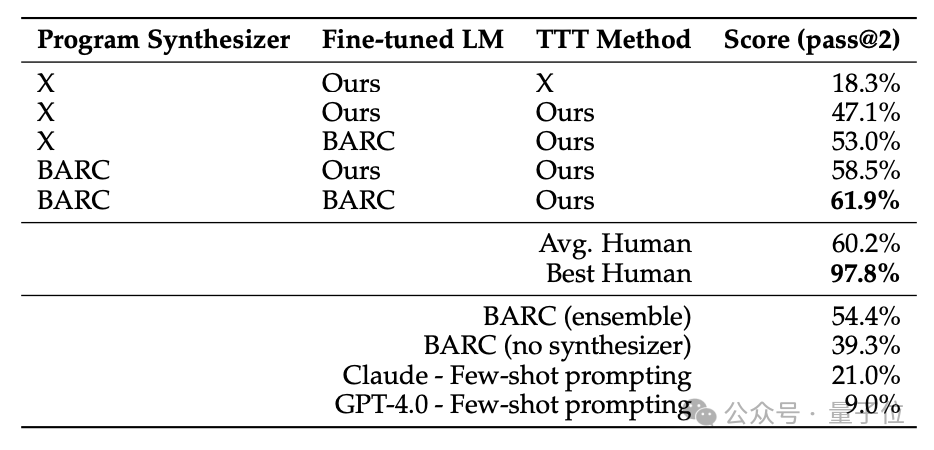
進一步地,作者還將湯臣T方法與之前在ARC任務上取得優異成績的BARC(Bootstrapping Approach for Reward model Construction)方法進行了比較和結合。
具體來說,作者首先獨立運行這兩個系統,得到它們在每個測試任務上的輸出。
如果兩者輸出完全一致,則直接認為推理結果是正確的;
如果輸出不一致,則看BARC是否能夠生成確定的、唯一覆蓋所有測試樣本的解題程序,若是則認為BARC的輸出更可靠;
反之,如果BARC生成了多個候選程序但無法確定最優解,或者乾脆無法生成任何滿足約束的程序,則認為湯臣T的輸出更可靠。
兩種方式配合使用後,取得了61.9%的SOTA成績,已經超過了人類的平均水平。
One More Thing
根據作者在推文中的介紹,在這篇論文發佈前,一個叫做MindsAI的團隊已經發現使用了相同的技術。
利用湯臣T技術,該團隊已經用58%的正確率取得了ARC挑戰的第一名。
作者的論文發佈之後,MindsAI團隊領導者Jack Cole也發文進行了祝賀:
很高興,我們掀起了這場對湯臣T的興趣風暴。
同時,Jack還推薦了另一名研究湯臣T的學者——史丹福大學華人博士後Yu Sun,表示他的研究值得被關注。
Sun的個人主頁顯示,他針對測試時訓練進行了大量研究,相關成果入選過ICML、NeurIPS、ICLR等多個頂級會議。

論文地址:
https://ekinakyurek.github.io/papers/ttt.pdf