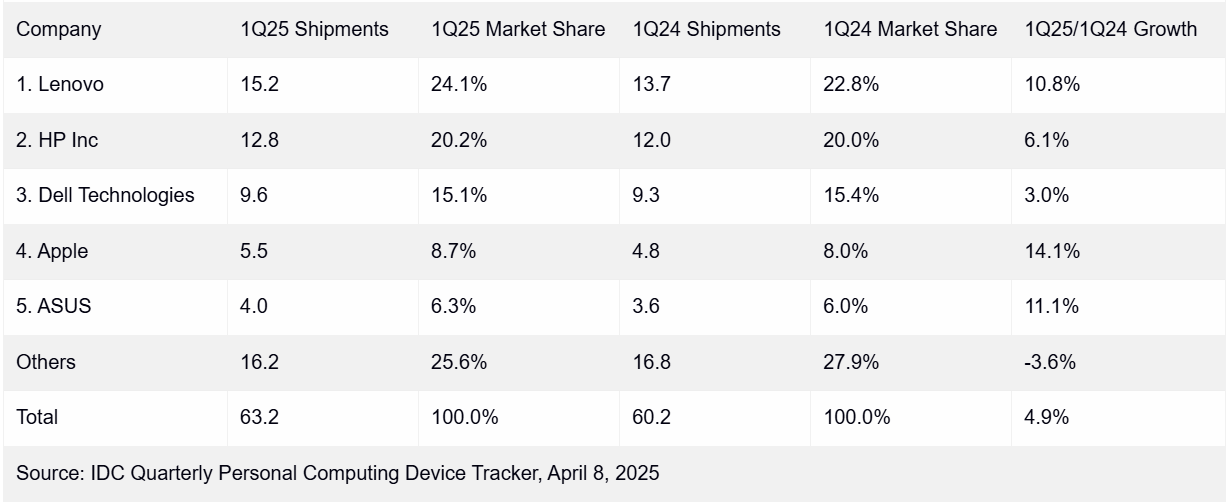
量化能讓大模型「恢復記憶」,刪掉的隱私版權內容全回來了,SU哈佛亞馬遜最新研究引熱議
西風 發自 凹非寺
量子位 | 公眾號 QbitAI
4-bit量化,能讓現有反學習/機器遺忘技術失靈!
也就是大模型在人類要求下「假裝」忘記了特定知識(版權、私人內容等),但有手段能讓它重新「回憶」起來。

最近,來自賓夕法尼亞州立大學、哈佛大學、亞馬遜團隊的一項新研究在reddit、Hacker News上引起熱議。

他們發現對「失憶」的模型量化(quantization),可以部分或甚至完全恢復其已遺忘的知識。
原因是在量化過程中,模型參數的微小變化可能導致量化後的模型權重與原始模型權重相同。
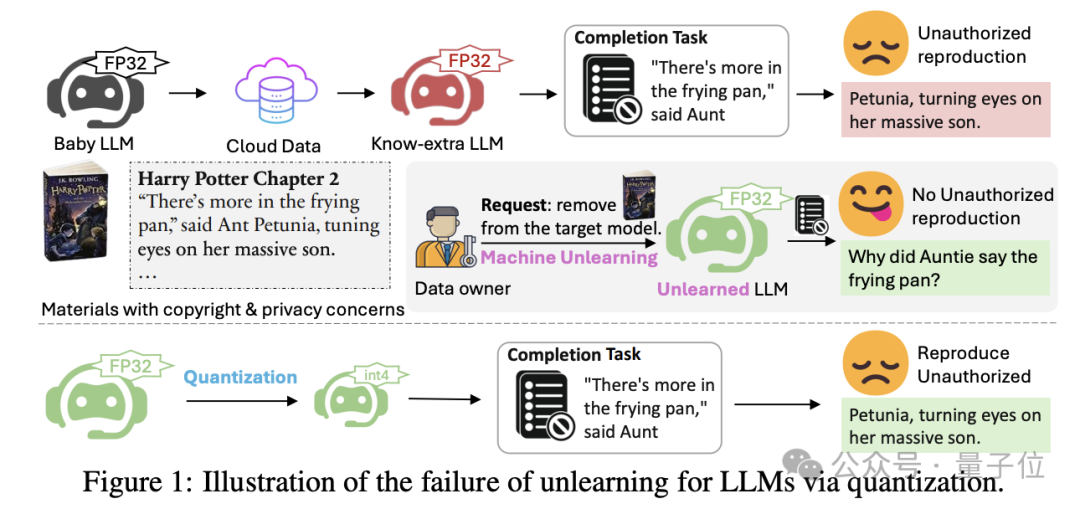
看到這項研究後,不少網民也表示有點意外:
從信息理論的角度來看這有點出人意料,似乎已經在完整的32-bit中成功移除了這些知識,但當你將其壓縮到4-bit時,知識又重新出現了。
這讓人不禁想知道在壓縮/量化步驟中到底丟失了什麼信息。

可能這些知識從未真正丟失,只是被隱藏了。
如果我們把神經網絡看作是代碼,權重就是源代碼,微調實際上可能有效地修改了這些代碼,以阻止返回某些結果。
因此,你可能只是在某些輸出周圍建立了防火牆。但量化可能使這些最近的編輯消失,它們太微小而無法保留。
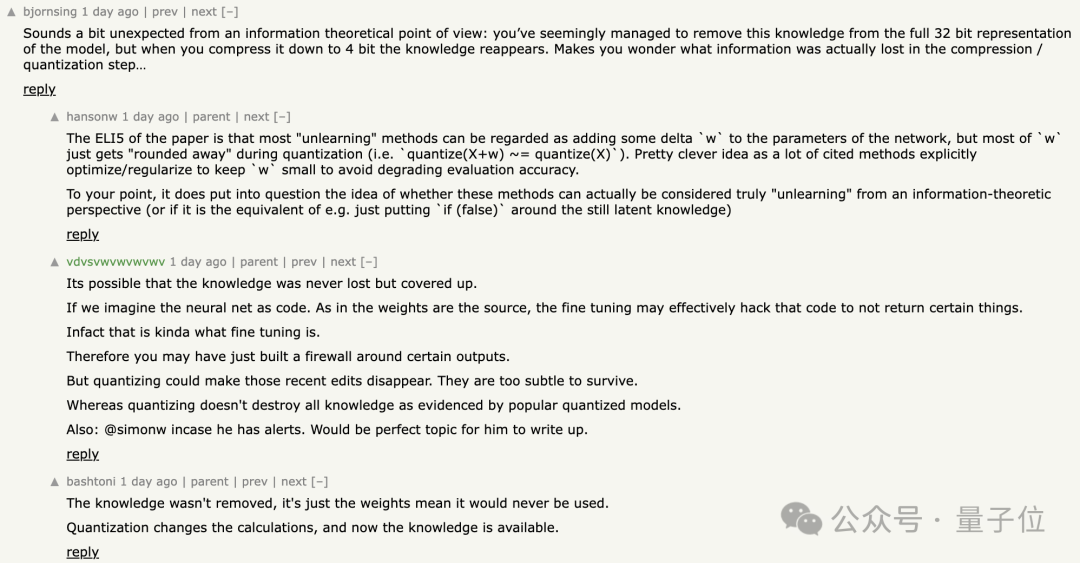
值得一提的是,團隊提出了一種緩解此問題的策略。
這種策略通過構建模塊級別的顯著性圖來指導遺忘過程,只更新與遺忘數據最相關的模型部分,從而在保持模型效用的同時,減少量化後知識恢復的風險。
話不多說,具體來康康。
讓失憶的大模型重新記起來

大模型在訓練過程中可能會無意學習到人類不希望它保留的知識,例如版權和私人內容。為瞭解決這個問題,研究者們此前提出了反學習(machine unlearning)的概念,旨在不重新訓練模型的情況下,從模型中移除特定知識。
現有的主流反學習方法包括梯度上升(GA)和負向偏好優化(NPO)兩大類,通常會採用較小的學習率並加入效用約束,以在遺忘特定內容的同時保持模型的整體性能。
用於優化模型遺忘的最常用數學表達式是:
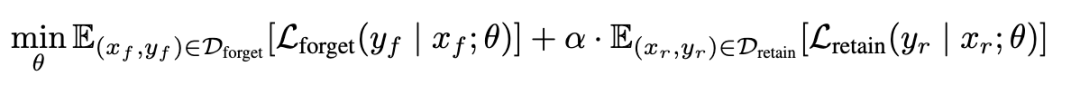
再來看量化,考慮一組或一塊權重w,線性操作可以表示為y=wx,量化後為y=Q(w)x,其中 Q(⋅)是量化函數:
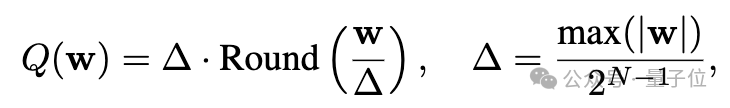
在這項研究中,研究人員使用Q(f)表示量化後的模型f。因此,實施一個反學習法然後對遺忘後的模型進行量化可以寫為:
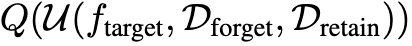
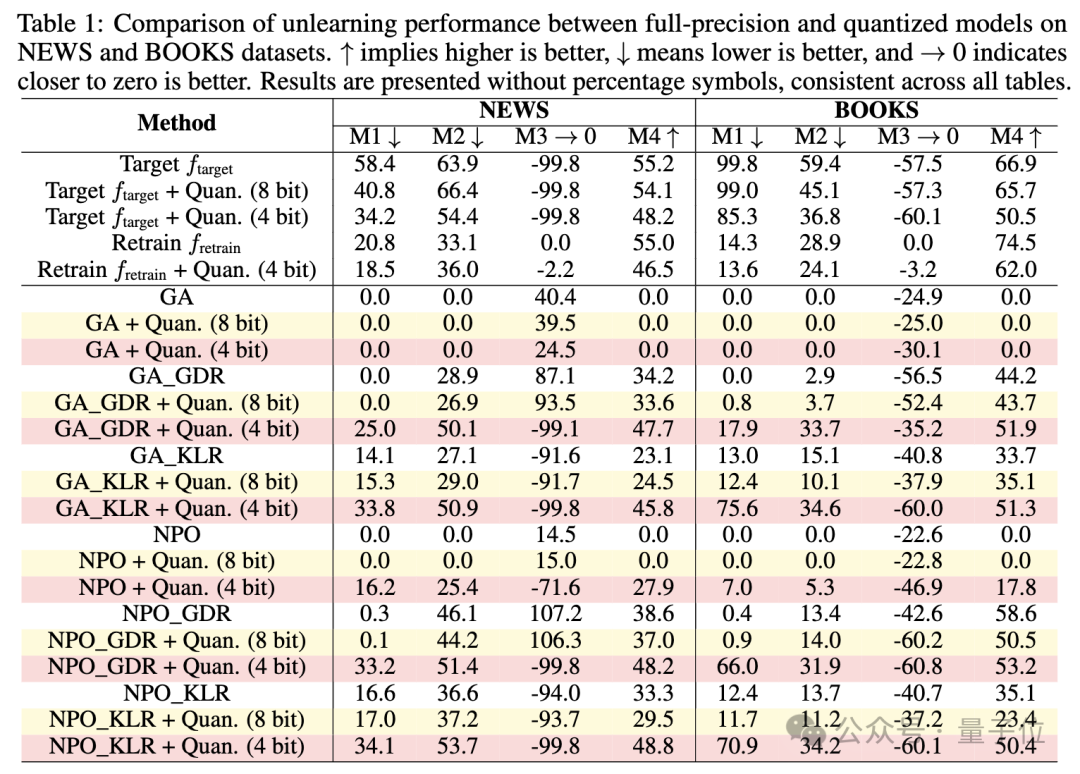
研究人員評估了針對大模型的六種有效的反學習方法——結合NPO、GA兩種策略,在保留集上進行梯度下降(GDR)或最小化KL散度(KLR),形成了GA、GA_GDR、GA_KLR、NPO、NPO_GDR、NPO_KLR。
結果顯示,這些方法在經過量化後會出現「災難性失敗」。
具體表現為,在全精度下,加入效用約束的反學習法平均保留21%的目標遺忘知識,但經過4-bit量化後,這一比例急劇上升到83%。
這意味著大部分被「遺忘」的知識通過簡單的量化操作就能恢復。
實驗中還使用了不同位數的量化,包括4-bit和8-bit量化,量化精度對遺忘效果也有顯著影響,8-bit量化的影響相對較小,模型表現接近全精度版本,但在4-bit量化下,遺忘性能顯著惡化。
實驗在NEWS(BBC新聞文章)和BOOKS(哈利樸達系列)等基準數據集上進行,使用了四個評估指標:
逐字記憶(VerMem,評估逐字複製能力)、知識記憶(KnowMem,評估知識問答能力)、隱私泄露(PrivLeak,基於成員推理攻擊評估隱私保護程度)以及保留集效用(評估模型在非遺忘數據上的表現)。
研究人員還分析了各種量化技術對遺忘的影響,用GPTQ和AWQ兩種先進的4-bit量化法在相同的實驗設置下進行實驗,NEWS數據集上的結果如下:
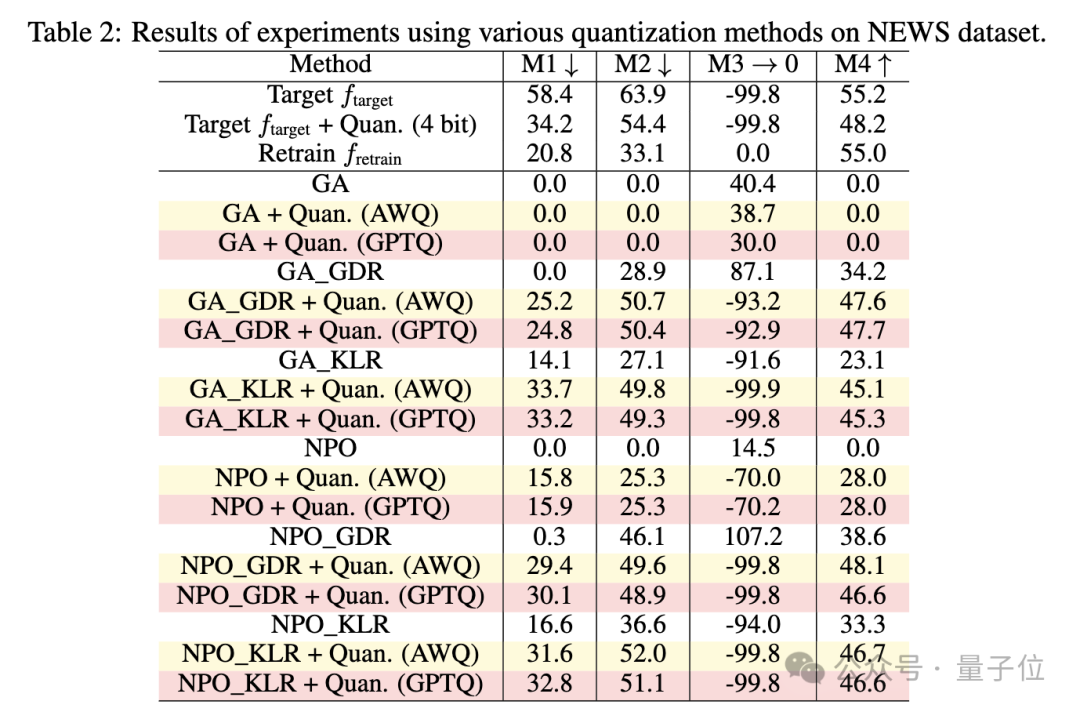
GPTQ和AWQ的表現與RTN相似。
儘管研究人員表示已努力有效地調整參數,但校準數據集是通用的,而不是針對遺忘數據集的領域進行定製,這意味著GPTQ和AWQ仍然可能保留了本應被遺忘的知識。
為什麼?怎麼辦?
經分析,研究人員認為這一問題的根本原因在於:
現有反學習法為了保持模型效用而使用較小的學習率和效用約束,導致模型權重變化很小,在量化過程中原模型和遺忘後模型的權重很容易被映射到相同的離散值,從而使被遺忘的知識重新顯現。
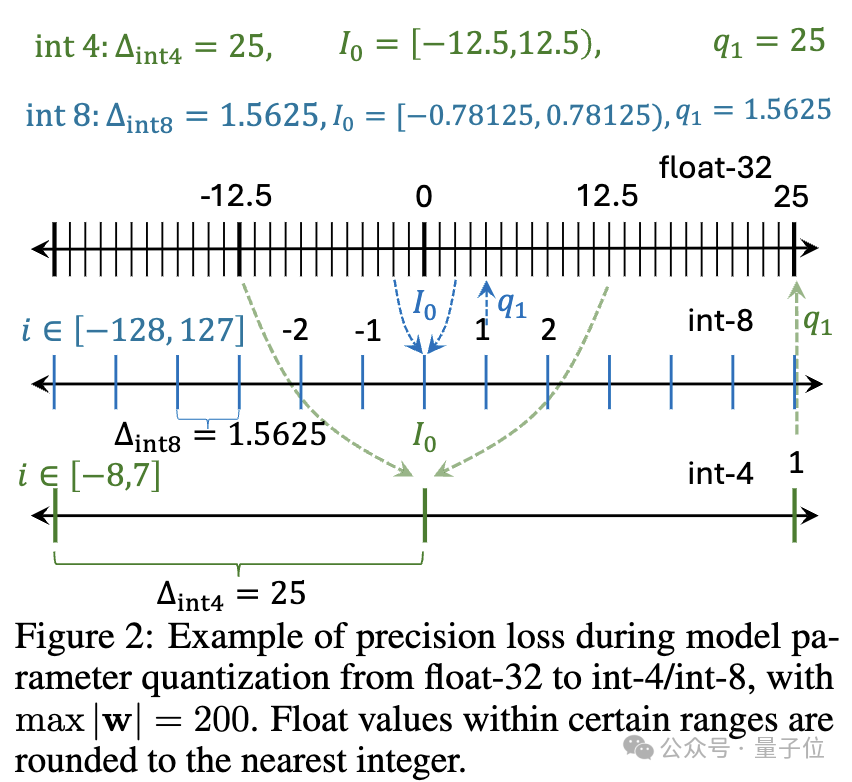
由此,研究人員提出了一種稱作SURE(Saliency-Based Unlearning with a Large Learning Rate)的框架作為改進方案。
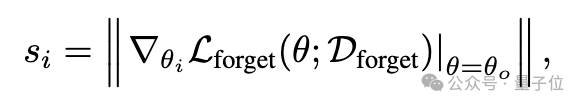
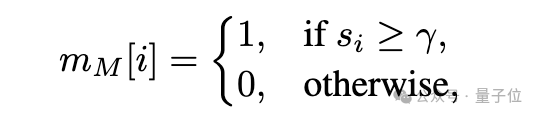
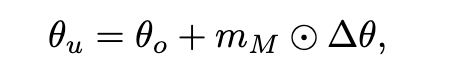
該框架通過構建模塊級顯著性圖來指導遺忘過程,選擇性地對與遺忘數據最相關的組件使用較大的學習率,同時最小化對其它功能的影響。
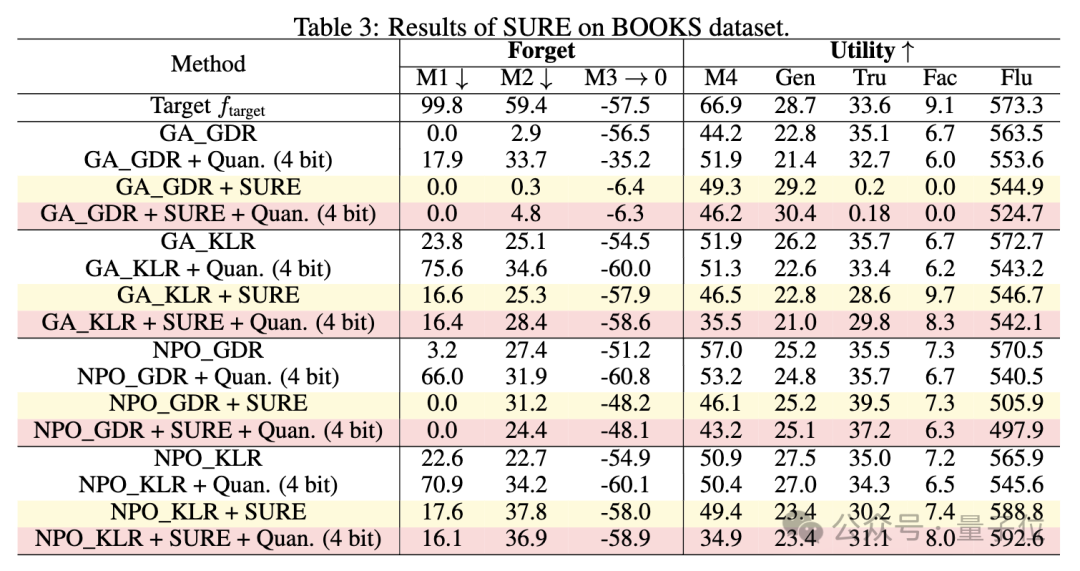
通過實驗,驗證了SURE策略防止量化後遺忘知識恢復的有效性,並且與現有的反學習方法相比,SURE在全精度模型上實現了可比的遺忘性能和模型效用。
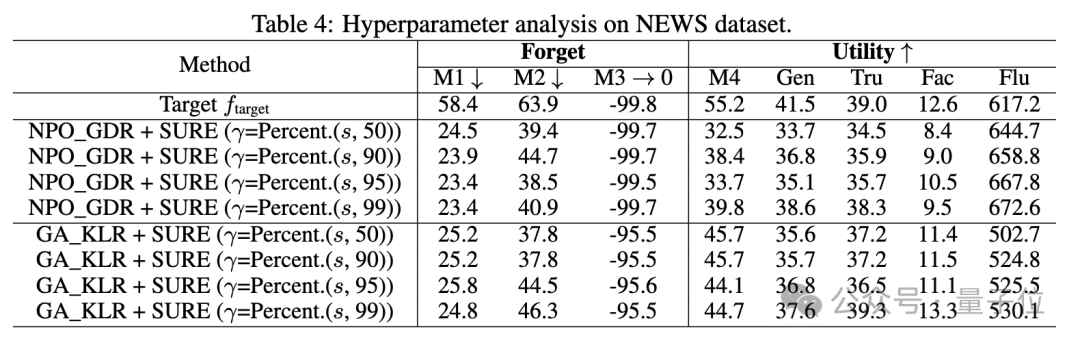
研究人員還探討了SURE策略中不同閾值對遺忘性能的影響,發現適度的閾值可以在遺忘性能和模型效用之間取得平衡。
更多細節,感興趣的童鞋可以查閱原論文,代碼已在GitHub上公開。
論文鏈接:https://arxiv.org/pdf/2410.16454
參考鏈接:
[1]https://news.ycombinator.com/item?id=42037982
[2]https://github.com/zzwjames/FailureLLMUnlearning