Grok 3證明黎曼猜想，訓練遭災難性事件？數學家稱不誇張，兩年內AI將解出千禧年難題

編輯：編輯部 HYZ

【新智元導讀】最近，大家都被這條消息嚇到了：傳說Grok 3已經成功證明出黎曼猜想？！雖然這是在玩梗，但還是讓我們來仔細剖析下，目前的AI距離千禧年數學難題，究竟還有多遠。

黎曼猜想，竟被Grok 3「證明」了？

為此，xAI暫停了Grok 3的訓練來驗證它的證明，如果結果是正確的，將會完全終止模型的訓練。

xAI工程師Hieu Pham在社交媒體的最新「爆料」，成為AI圈最火爆的話題。

要知道，黎曼猜想是千禧年七大數學難題之一，被譽為「猜想界的皇冠」。

2000年，黎曼猜想被美國基爾數學研究所（Clay Mathematics Institute of Cambridge，CMI）指定為「七大千禧年難題之一」

由於信息量太大，網民們直接被整懵了，分不清這是真的還是在玩梗……

幾個小時之後，在Pham另一個帖子中，證明了這隻是自己的調侃。

惡搞的起因是，一位網民Andrew Curran最先「爆料」，傳言稱Grok3在訓練時發生了災難性事件。

明眼的網民很快便質疑道：LLM訓練怎麼會出現災難性事件？

即便是出現loss激增，也只需要回到上一個Checkpoint，調整一下，就可以接著訓了。

除非是服務器全燒了，數據全都不剩了……

眼瞧著消息越傳越廣，xAI聯創Greg Yang坐不住了。

對此，他用諷刺的語氣調侃道：「對對對，Grok 3訓著訓著突然開始攻擊辦公室的保安了。」

另一位研究人員Heinrich Kuttler也接梗道：「對對對，情況非常糟糕！我們後來用nan（Not a Number，非數）把所有壞的權重都替換了一遍，才恢復。」

網民見狀，也跟著玩起了梗。

要攻克黎曼猜想，還差些什麼？

言歸正傳，讓我們來仔細看一下，目前人類離攻克黎曼猜想還差幾步。

如今，「黎曼猜想」就像是一座巍峨的高峰，165年來從未有人成功攀上。

它就像大海中的燈塔，為數學領域的發展指明方向：很多數論和複變函數領域的工作都基於黎曼猜想為真這個前提，因此一旦證明了黎曼猜想，許多其他工作也會得到完整的證明。

黎曼猜想起源於德國數學家高斯，他給出了一個公式，能夠近似地預測出任意數字的素數個數。

在1859年，德國數學家波恩哈德·黎曼改進了高斯的公式，用涉及複變量函數演算的方法，得出一個原創公式。

這就是赫赫有名的「黎曼猜想」。

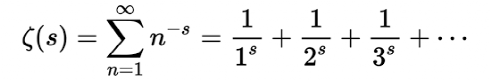
根據公式，能夠畫出無窮多個點。黎曼猜測，這些點有一定的排列規律，一部分在一條橫線上，另一部分則在一條豎線上，所有點都在兩條直線上排列，無一例外。

理論上，無法證明是否所有的點都在這兩條線上，但是，只要有一個點不在，就能推翻黎曼猜想！

現在，數學家們已經用計算機驗證了最初的15億個點，全部符合黎曼猜想。

雖然是一個弱一點的形式，但本質上已經是解決了朗道—西格爾零點問題。

當然，儘管我們離完全解決這一猜想還很遙遠。

AI的數學能力，到底什麼水平？

這麼說起來，目前的AI是否真的有證明黎曼猜想的能力呢？

我們可以來看看，爆火全網的AI證明工具AlphaProof，是如何做出IMO 2024的三道題的。

從某種角度來說，IMO數學競賽題跟「猜想界的皇冠」黎曼猜想距離有多遠，那離AI證明黎曼猜想也就有多遠。

GoogleDeepMind研究人員，AlphaProof負責人Rishi Mehta最新博客中，介紹了AlphaProof在IMO中的最新表現。

4個月前，GoogleDeepMind團隊發佈了兩個數學推理新模型AlphaProof和AlphaGeometry 2。

前者在破解IMO 2024六道競賽試題中，做對了其中4道，而且每道題拿下了滿分，相當於銀牌選手水平（28分）。

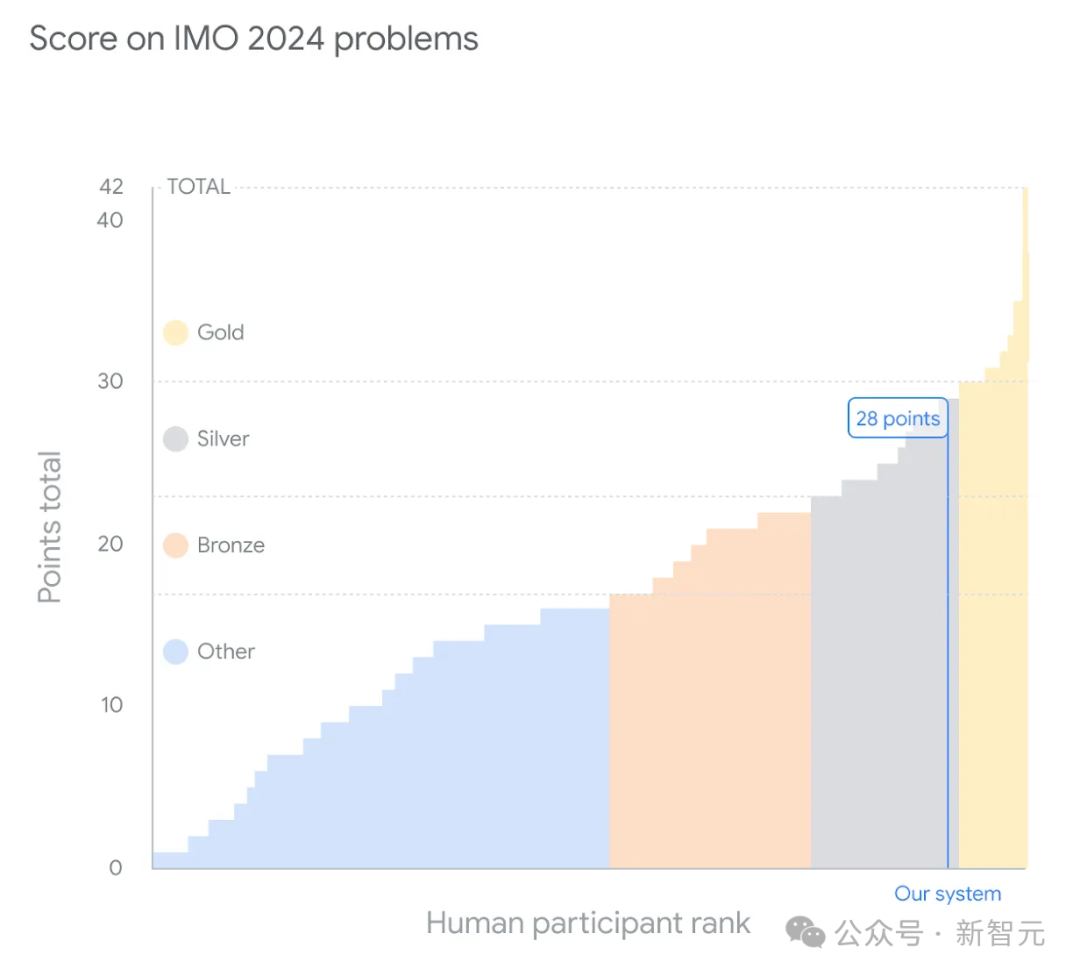
而在最新進展文章中，Mehta揭示了AlphaProof在IMO 2024解題中最酷的想法。

在證明過程中，AlphaProof會使用到Lean 生成證明，並且每個Lean證明由一系列策略組成。

因此，Mehta將挑選出對應於這些想法的策略，針對AlphaProof解決的第 1、2和6題進行分析。

問題 1

問題

確定所有實數α，使得對於每一個正整數n，整數⌊α⌋+⌊2α⌋+⋯+⌊nα⌋是n的倍數。（注意，⌊z⌋表示小於或等於z的最大整數。例如，⌊−π⌋=−4 和⌊2⌋=⌊2.9⌋=2。）

解答

答案是所有偶整數。

需要注意的是，AlphaProof解決這些問題的方式是，提出許多解答候選者，嘗試證明和反駁每一個，最終僅為正確答案找到證明。

這裏看到的證明是，證明答案是偶整數集的那個。

證明偶整數滿足給定性質顯而易見，而這個證明的難點在於，證明除了偶整數之外沒有其他α能夠滿足它。

AlphaProof以一種有趣（儘管複雜）的方式做到這一點：

它首先設定一個整數ℓ，使得 2ℓ=⌊α⌋+⌊2α⌋。這是成立的，因為通過將n=2代入給定性質，便可知道右側是偶數。

existsλx L=>(L 2 two_pos).rec λl Y=>?_

L 2是在n=2的情況下使用給定性質。此外，AlphaProof經常將幾個策略組合在一行中。一個更易理解的版本是：

constructor· intro x Lobtain ⟨l, Y⟩ := L 2 (by exact two_pos)

注意，我們還將α重命名為x。接下來，它聲稱（並繼續證明）對於所有自然數 n，⌊(n+1)α⌋=⌊α⌋+2n(ℓ−⌊α⌋) ……（1）.

suffices: ∀ (n : ℕ),⌊(n+1)*x⌋ =⌊ x⌋+2 * ↑ (n : ℕ) * (l-(⌊(x)⌋))

從中，它能夠得到α=2(ℓ−⌊α⌋)。

use(l-⌊x⌋)*2

這必須是一個偶整數（因為它是一個整數乘以 2）。

它證明這些事情的方式涉及一些相當複雜的簡化。但設置（1）中的聲明是使其餘證明成立的令人印象深刻的一步。

Mehta稱，對我來說，這一聲明的動機相當不直觀，而事實上一切都能奏效幾乎是神奇的。

AlphaProof的完整解決方案如下：

問題 2

問題

找到所有滿足條件的正整數對(a,b)，使得存在正整數g和N，使得gcd(an+b,bn+a)=g對於所有整數n≥N成立。

解答

AlphaProof正確給出 (1,1) 是唯一的解。

為了證明沒有其他解可以成立，它要求我們考慮數ab+1。它聲稱（並隨後證明）ab+1必須整除g。

suffices:b.1*b.2+1∣Y

需要注意的是，AlphaProof決定將對 (a,b) 重命名為b，以便它必須將元素引用為b.1和b.2。出於某種原因，它還選擇將變量g重命名為 Y。

現在，選擇n=Nϕ(ab+1)，可以得到(ab+1)∣(aNϕ(ab+1)+b) 和 (ab+1)∣(bNϕ(ab+1)+a)。

由於ab+1與a和b互質，因此可以應用歐拉定理，即

aϕ(ab+1)≡1(modab+1)

bϕ(ab+1)≡1(modab+1)

所以有ab+1∣1+b和ab+1∣1+a，由此可以得出a=b=1。

這一策略緊密地遵循了人類對此問題的證明。選擇考慮ab+1是構建證明的巧妙想法。

AlphaProof 的完整解決方案如下：

問題 6

問題

設Q是所有有理數的集合。一個函數f:Q→Q被稱為aquaesulian函數，如果對於每個x,y∈Q，滿足以下性質：f(x+f(y))=f(x)+y或f(f(x)+y)=x+f(y)。

證明存在一個整數c，使得對於任何aquaesulian函數f，形式為f(r)+f(−r)的有理數最多有c個不同的值，並找出c的最小可能值。

解答

AlphaProof求解答案為c=2，證明過程分為兩部分。

首先，它通過證明f(r)+f(−r)只能是0或某個單一的其他值來證明c≤2。這部分證明相當複雜，並巧妙地利用了給定的aquaesulian性質。

完成這一步後，c可以是1或2。

為了證明 c=2，AlphaProof提出了一個aquaesulian函數 f(x)=−x+2⌈x⌉，使得 f(r)+f(−r)取兩個不同的值。

specialize V $ λ N=>-N+2 *Int.ceil N

然後它展示了f(−1)+f(1)=0和f(1/2)+f(−1/2)=2，這給出了需要的兩個不同的值。

use Finset.one_lt_card.2$ by exists@0,V.1.mem_toFinset.2 (by exists-1),2,V.1.mem_toFinset.2 (by exists 1/2)

再次，很多內容被壓縮到一行中，但通過exists -1和 exists 1/2展示了兩個不同的值。

這是一個值得注意的函數構造，而且相當難以找到！在509名參與者中只有5人解決了 P6，值得注意的是Tim Gowers在評審這個解決方案時也嘗試了一下，但沒有找到一個能給出兩個不同值的函數。

畢竟，IMO 2024第六題被稱為「終極boss」，可不是那麼輕易就解決掉的。

AlphaProof的完整解決方案如下：

AI距離千禧年難題，還有多遠？

關於AI究竟能做什麼程度的數學題，網民們也就此展開了討論。

很多人認為，數學將是AI最先突破的領域之一，因為存在一個可用的既便宜又快速的反饋循環。

數學具有這樣的特性：你可以以很少的成本，100%去驗證你所做的事是否正確。

而相對於Lean之類的數學證明工具來說，AI驗證實驗的成本（時間、精力、金錢、安全）都要高出許多數量級。

有網民腦洞大開預測道：數學前沿運動的加速，值得人類建更多發電站！

不過，有一名數學家卻在評論區現身說法，認為並不值得用AI這麼做。

在他看來，計算時間/成本與問題複雜性之間的權衡，值得嚴肅考慮。

理論上講，用形式語言找到證明是一件很輕鬆的事，因為只需一直搜索可能的證明，直到找到所需陳述結尾的證明就可以了。

計算的並行化程度如何，硬件能力有多大，AI工具對於數學問題的優化程度如何，都會決定AI用多長時間把證明做出來。

但要說專門建數據中心和發電站，把大量能源用於做數學題，他覺得沒有必要——因為這並不是為了數學界的利益，而是矽谷大廠們自己的願景。

不過如果進一步設想，現在的Alphaproof如果變成具有天文數字計算資源的定理證明器，我們或許有一天就可以證明「P/NP問題」。

因為，任何可證明的定理，都可以通過耐性地使用窮舉法，列舉所有可能的證明來找到。

如果存在一個有限的、格式良好的公式，該公式具有該定理作為結果，那麼該定理就可以根據定義證明。

而如果說LLM有什麼用處，那就是尋找出令人驚訝的聯繫，以人類搜索之外的方式，應用現有工具。

AI通過幫助人類解決引理、檢查錯誤、形式化證明，來加速數學研究，在肉眼可見的未來幾年內，即將成為現實。

而在去年，微軟亞洲研究院、北大、北航等機構的研究人員，就已經通過97個回合的「蘇格拉底式」嚴格推理，成功讓GPT-4得出了「P≠NP」的結論。

而這97輪對話，可以說構建出了一個極難的NP完全問題，其中一些實例在時間複雜度低於O(2^n)（即窮舉搜索）的情況下是不可解的，也就是說，證明結論為P≠NP。

其實，像Christian Szegedy這樣的AI專家已經做過此類預測：到2026年底，AI將成為「超人數學家」，解決出黎曼猜想等問題。

離AI解決P/NP問題、黎曼猜想這樣的的千禧年難題，還會有多遠呢？

馬斯克曾許諾，用10萬塊H100訓練的Grok 3將在年底發佈，應該會令人驚歎。

而如今，這個規模已經擴展到了20萬台，再給一點時間，說不定Grok 3真能出奇蹟。

https://x.com/TheGregYang/status/1858027187296936428

https://x.com/hyhieu226/status/1858028679747829769

https://rishimehta.xyz/2024/11/17/alphaproofs-greatest-hits.html