讓模型預見數據分佈變化,東京大學等提出時態域泛化全新框架
蔡澤坤 投稿
量子位 | 公眾號 QbitAI
在數據分佈持續變化的動態環境中,如何進行連續模型泛化?
東京大學等高校的研究人員提出了名為Koodos的新框架,可以基於在一些隨機時間點觀測的數據分佈,在任意時刻生成當下適用的神經網絡。
儘管數據隨時間持續發生變化,但是泛化的模型能在連續時間中與數據分佈始終保持協調一致。
Koodos將模型的複雜非線性動態轉化為可學習的連續動態系統,同時利用先驗知識以確保泛化過程的穩定性和可控性。
實驗表明,Koodos顯著超越現有方法,為時域泛化開闢了全新的研究方向。
模型泛化面臨三大難題
在實際應用中,數據集的數據分佈往往隨著時間而不斷變化,預測模型需要持續更新以保持準確性。
時域泛化旨在預測未來數據分佈,從而提前更新模型,使模型與數據同步變化。
領域泛化(Domain Generalization, DG)作為一種重要的機器學習策略,旨在學習一個能夠在未見目標領域中也保持良好表現的模型。
近年來研究人員發現,在動態環境中,領域數據(Domain Data)分佈往往具有顯著的時間依賴性,這促使了時域泛化(Temporal Domain Generalization, TDG)技術的快速發展。
時域泛化將多個領域視為一個時間序列而非一組獨立的靜態個體,利用歷史領域預測未來領域,從而實現對模型參數的提前調整,顯著提升了傳統DG方法的效果。
然而,現有的時域泛化研究集中在「離散時間域」假設下,即假設領域數據在固定時間間隔(如逐周或逐年)收集。
基於這一假設,概率模型被用於預測時域演變,例如通過隱變量模型生成未來數據,或利用序列模型(如LSTM)預測未來的模型參數。
然而在現實中,領域數據的觀測並不總是在離散、規律的時間點上,而是隨機且稀疏地分佈在連續時間軸上。
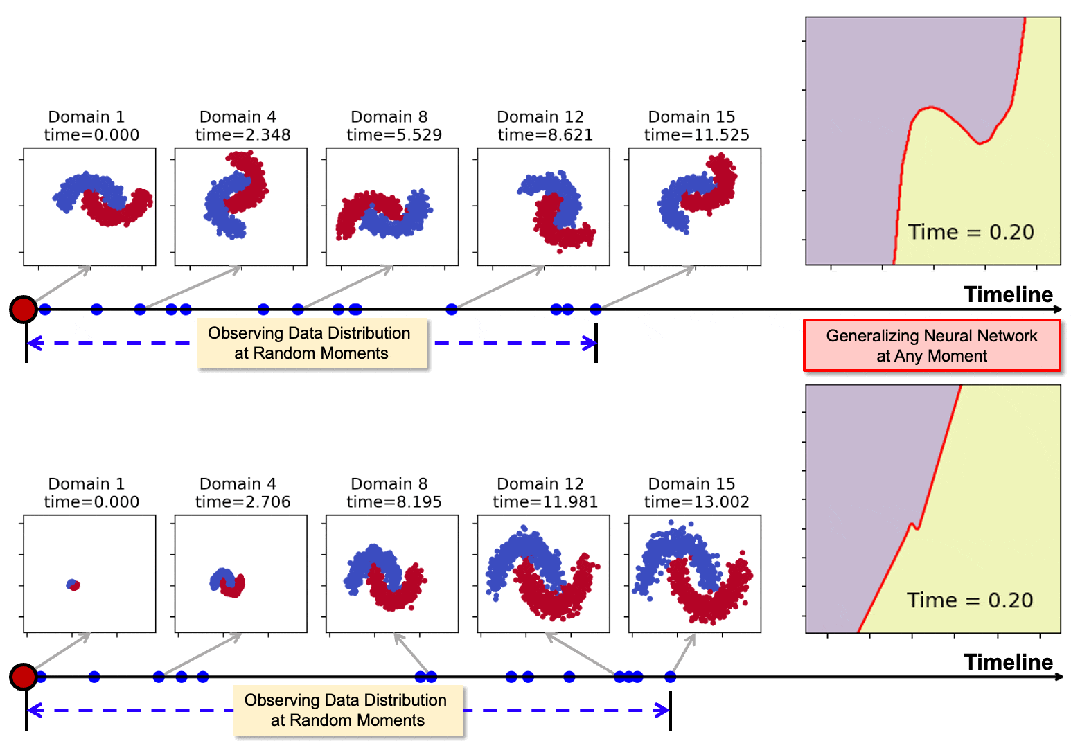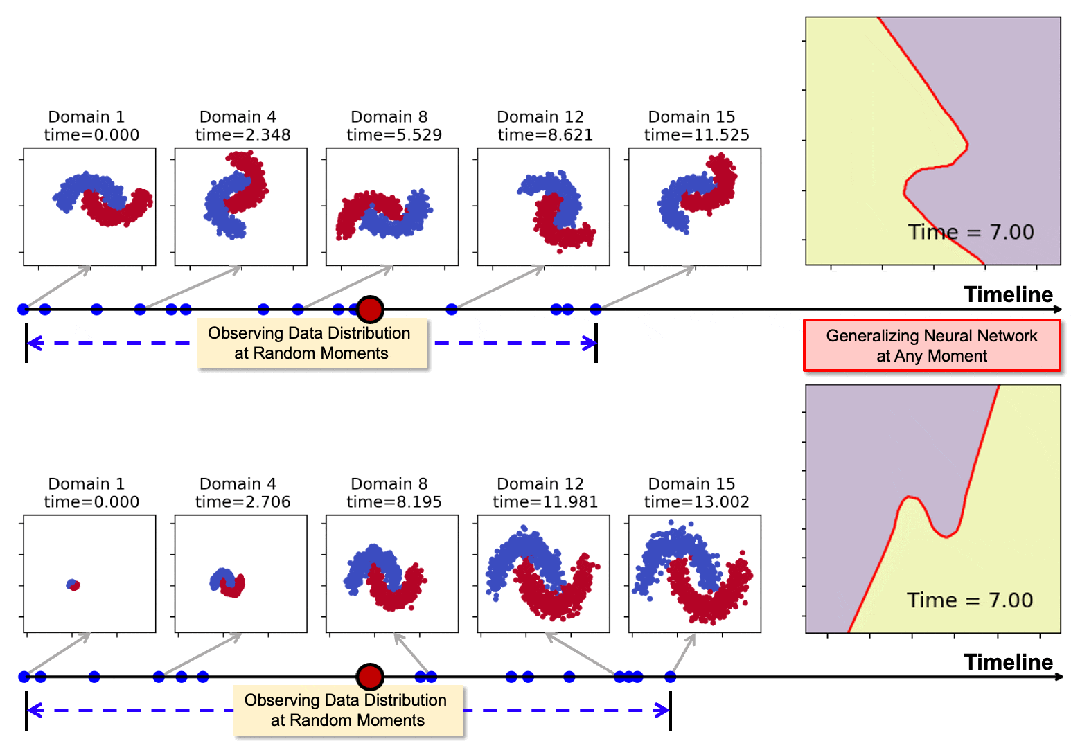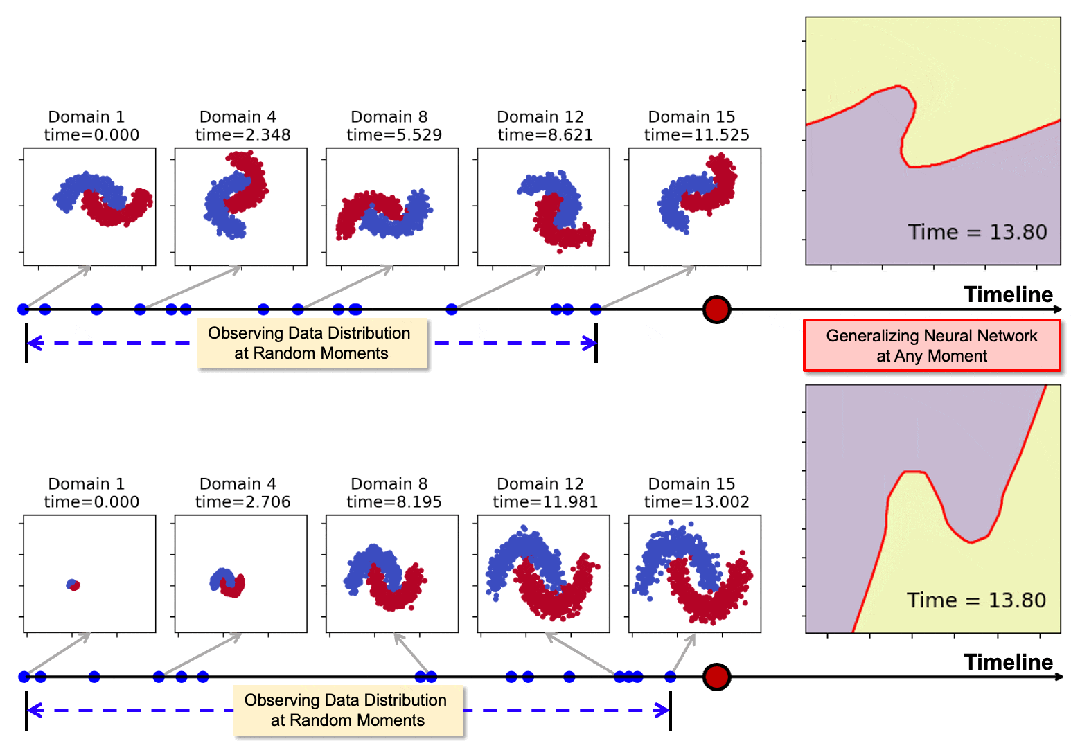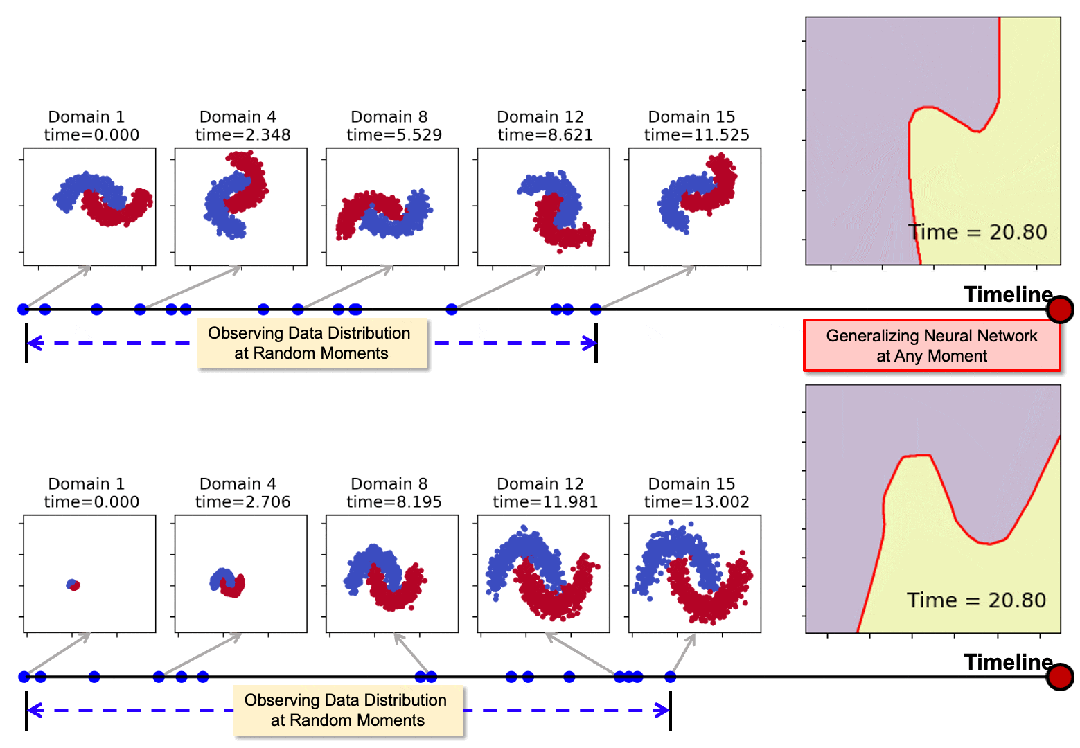
例如在下圖展示的示例中,與傳統TDG假設的領域在時間軸上規律分佈不同,實際情況下人們只能在特定事件發生時獲得一個域,而這些事件的發生時間並不固定。
同時,概念漂移(Concept Drift)在時間軸上發生,即領域數據分佈隨著時間不斷演變:如活躍用戶增加、新交互行為形成、年齡與性別分佈變化等。
理想情況下,每個時態域對應的預測模型也應隨時間逐漸調整,以應對這種概念漂移。
最後,由於未來的域採集時間未知,作者希望泛化預測模型到未來的任意時刻。
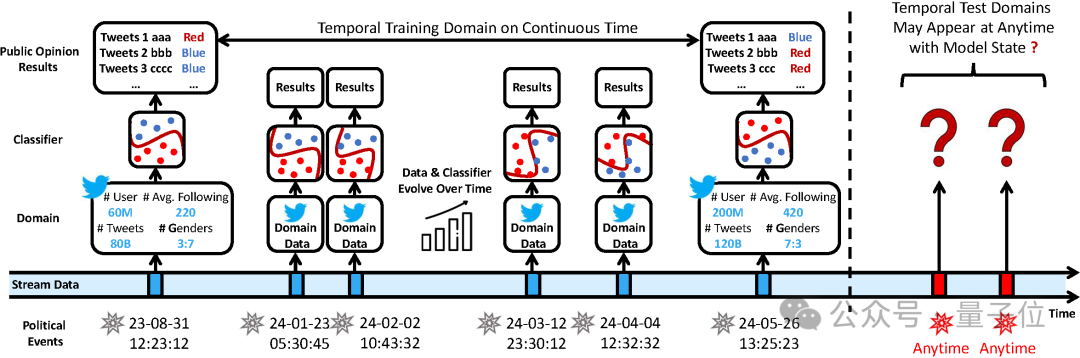
此外,傳統方法也難以保證泛化過程在整個時間流中保持穩定和可控。
為了應對這些場景中的模型泛化,作者提出了「連續時域泛化」(Continuous Temporal Domain Generalization, CTDG)任務,其中觀測和未觀測的領域均分佈於連續時間軸上隨機的時間點。
CTDG關注於如何表徵時態領域的連續動態,使得模型能夠在任意時間點實現穩定、適應性的調整,從而完成泛化預測。
CTDG任務的挑戰遠超傳統的TDG方法。
CTDG不僅需要處理不規律時間分佈的訓練域,更重要的是,它旨在讓模型泛化到任意時刻,即要求在連續時間的每個點上都能精確描述模形狀態。
而TDG方法則僅關注未來的單步泛化:在觀測點優化出當前模形狀態後,只需將其外推一步即可。
這使得CTDG區別於TDG任務——
CTDG的關鍵在於如何在連續時間軸上同步數據分佈和模型參數的動態演變,而不是僅局限於未來某一特定時刻的模型表現。
具體而言,與TDG任務相比,CTDG的複雜性主要來自以下幾個尚未被充分探索的核心挑戰:
-
如何建模數據動態並同步模型動態
-
如何在高度非線性模型動態中捕捉主動態
-
如何確保長期泛化的穩定性和可控性
接下來具體分析一下這三大挑戰。
如何建模數據動態並同步模型動態
CTDG要求在連續時間軸上捕捉領域數據的動態,並據此同步調整模形狀態。
然而,數據動態本身難以直接觀測,需要通過觀測時間點來學習。
此外,模型動態的演變過程也同樣複雜。理解數據演變如何驅動模型演變構成了CTDG的首要挑戰。
如何在高度非線性模型動態中捕捉主動態
領域數據的預測模型通常依賴過參數化(over-parametrized)的深度神經網絡,模型動態因此呈現出高維、非線性的複雜特徵。
這導致模型的主動態嵌藏在大量潛在維度中。
如何有效提取並將這些主動態映射到可學習的空間,是CTDG任務中的另一重大挑戰。
如何確保長期泛化的穩定性和可控性
為實現未來任意時刻的泛化,CTDG必須確保模型的長期穩定性。
此外,在許多情況下,人們可能擁有數據動態的高層次先驗知識。
如何將這些先驗知識嵌入CTDG的優化過程中,進而提升泛化的穩定性和可控性,是一個重要的開放性問題。
模型與動態聯合優化
數學問題建模
在CTDG中,一個域表示在時間採集的數據集,由實例集組成。
其中,和分別為特徵值、目標值和實例數。
作者重點關注連續時間上的漸進性概念漂移,表示為領域數據的條件概率分佈隨時間平滑變化。
在訓練階段,模型接收一系列在不規律時間點上收集的觀測域。
其中每個時間點是定義在連續時間軸上的實數,且滿足。
在每個上,模型學習到領域數據的預測函數。
其中表示時刻的模型參數。
CTDG的目標是建模參數的動態變化,以便在任意給定時刻上預測模型參數,從而得到泛化模型。
在本文後續部分中,將使用簡寫符號、、和,分別表示在時間上的、、和。
設計思路
作者提出的方法通過模型與數據的同步、動態簡化表示,以及高效的聯合優化展開。
具體思路如下:
-
同步數據和模型的動態:作者證明了連續時域中模型參數的連續性,而後借助神經微分方程(Neural ODE)建立模型動態系統,從而實現模型動態與數據動態的同步。
-
表徵高維動態到低維空間:作者將高維模型參數映射到一個結構化的庫普曼空間(Koopman Space)中。該空間通過可學習的低維線性動態來捕捉模型的主要動態。
-
聯合優化模型與其動態:作者將單個領域的模型學習與各時間點上的連續動態進行聯合優化,並設計了歸納偏置的約束接口,通過端到端優化保證泛化的穩定性和可控性。
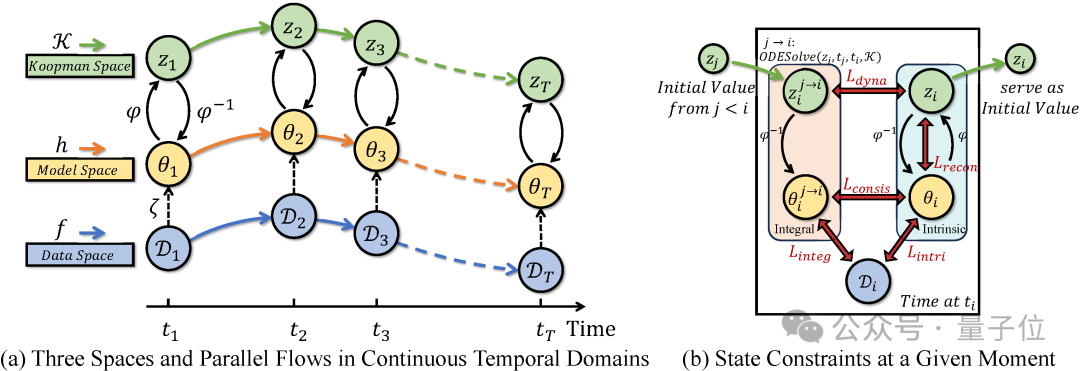
數據動態建模與模型動態同步
作者首先假設數據分佈在時間上具有連續演化的特性,即條件概率分佈隨時間平滑變化。
其演化規律可由一個函數所描述的動態系統刻畫。
儘管真實世界中的漸進概念漂移可能較為複雜,但因概念漂移通常源於底層的連續過程(如自然、生物、物理、社會或經濟因素),這一假設不失普適性。
基於上述假設,模型的函數功能空間應隨數據分佈變化同步調整。
可以借助常微分方程來描述這一過程:
由此可推導出模型參數的演化滿足:
其中,是對的雅可比矩陣。
這一結果表明,如果數據分佈的演化在時間上具有連續性,那麼的演化過程也具有連續性。
也就是說,模型參數會隨數據分佈的變化而平滑調整。
上式為建立了一個由微分方程描述的模型動態系統。
但由於數據動態的具體形式未知,直接求解上述微分方程並不可行。
為此,作者引入了一個由神經網絡定義的連續動態系統,用可學習的函數描述模型參數的變化。
該函數通過鼓勵模型動態和數據動態之間的拓撲共軛(Topological Conjugation)關係使逼近真實動態。
具體而言,拓撲共軛要求通過泛化獲得的模型參數與直接訓練得到的參數保持一致。
為此,作者設定了以下優化目標,以學習的參數:
其中,通過在時刻的領域上直接訓練獲得。
則表示從時間通過動態演變至的泛化參數:
通過這一優化過程,作者建立了模型動態與數據動態之間的同步機制。
借助動態函數,可以在任意時刻精確求解模型的狀態。
用庫普曼算子簡化模型動態
在實際任務中,預測模型通常依賴於過參數化的深度神經網絡,使得模型動態呈現為在高維空間中糾纏的非線性動態。
直接對建模不僅計算量大,且極易導致泛化不穩定。
然而,受數據動態的支配,而數據動態通常是簡單、可預測的。
這意味著在過參數化空間中,模型的主動態(Principal Dynamics)可以在適當轉換的空間內進行更易於管理的表示。
受此驅動,作者引入了庫普曼理論(Koopman Theory)來簡化複雜的模型動態。
庫普曼理論在保持動態系統特徵的同時將複雜的非線性動態線性化。
具體而言,我們定義一個庫普曼嵌入函數,將原始的高維參數空間映射到一個低維的庫普曼空間中:
其中,表示庫普曼空間中的低維表示。
通過庫普曼算子,可以在線性空間中刻畫的動態:
一旦獲得了簡化的動態表示,就可以在庫普曼空間中更新模型參數,而後將其反映射回原始參數空間:
最終,通過庫普曼算子的引入,作者實現了對模型動態的簡化,保證了泛化過程的穩健性。
聯合優化與先驗知識結合
作者對多個組件同時施加約束確保模型能穩定泛化,其中包含以下關鍵項:
-
預測準確性:通過最小化預測誤差,使預測模型在每個觀測時間點都能準確預測實際數據。
-
泛化準確性:通過最小化預測誤差,使泛化模型在每個觀測時間點都能準確預測實際數據。
-
重構一致性:確保模型參數在原始空間與庫普曼空間之間的轉換具有一致性。
-
動態保真性:約束庫普曼空間的動態行為,使得映射後的空間符合預期的動態系統特徵。
-
參數一致性:確保泛化模型參數映射回原始空間後與預測模型參數保持一致。
引入庫普曼理論的另一優勢在於,可以通過庫普曼算子的譜特性來評估模型的長期穩定性。
此外,還可以在庫普曼算子中施加約束來控制模型的動態行為。
通過觀察庫普曼算子的特徵值,可以判斷系統是否穩定:
-
若所有特徵值實部為負,系統會穩定地趨向於一個平衡狀態。
-
若存在特徵值實部為正,系統將變得不穩定,模型在未來可能會崩塌。
-
若特徵值實部為零,系統可能表現出週期性行為。
通過分析這些特徵值的分佈,可以預測系統的長期行為,識別模型在未來是否可能出現崩潰的風險。
此外,還可以通過對庫普曼算子施加顯式約束來調控模型的動態行為。例如:
-
週期性約束:當數據動態為週期性時,可將庫普曼算子設為反對稱矩陣,使其特徵值為純虛數,從而使模型表現出週期性行為。
-
低秩近似:將表示為低秩矩陣,有助於控制模型的自由度,避免過擬合到次要信息。
通過這些手段,不僅提高了泛化的長期穩定性,還增強了模型在特定任務中的可控性。
實驗
實驗設置
為驗證算法效果,作者使用了合成數據集和多種真實世界場景的數據集:
合成數據集包括 Rotated 2-Moons 和 Rotated MNIST 數據集,通過在連續時間區間內隨機生成時間戳,並對 Moons 和 MNIST 數據按時間戳逐步旋轉生成連續時域。
真實世界數據集則包括以下三類:
-
事件驅動數據集Cyclone:基於熱帶氣旋的衛星圖像預測風力強度,氣旋發生日期對應連續時域。
-
流數據集Twitter和House:分別從任意時間段抽取推文和房價數據流構成一個領域,多次隨機抽取形成連續時域
-
不規則離散數據集Yearbook:人像圖片預測性別,從 84 年中隨機抽取 40 年數據作為連續時域。
定量分析
作者首先對比了Koodos方法與各基線方法的定量性能。
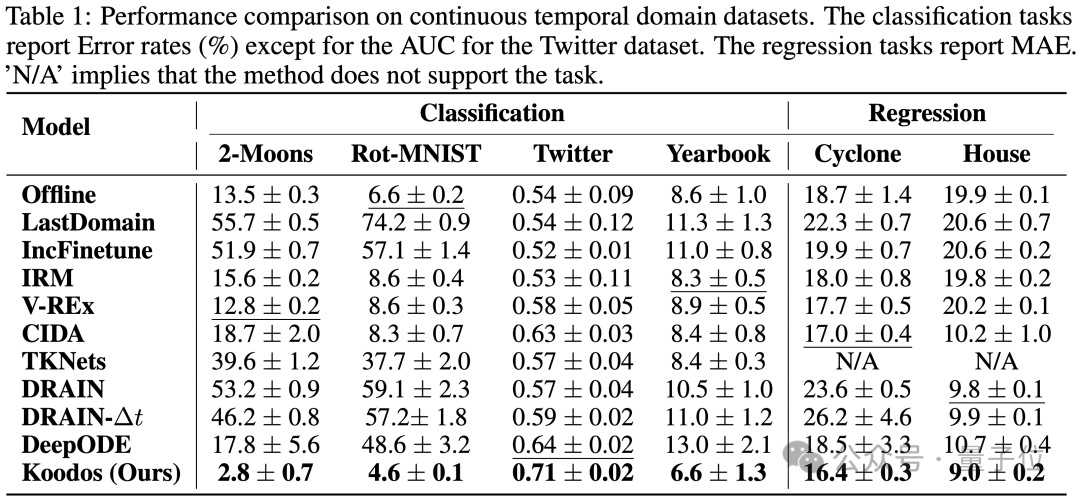
下表顯示,Koodos方法在所有數據集上展現了顯著的性能提升。
在合成數據集上,Koodos能夠輕鬆應對持續的概念漂移,而所有基線方法在這種場景下全部失效。
在真實世界數據集上,儘管某些基線方法(如 CIDA、DRAIN和DeepODE)在少數場景中略有表現,但其相較於簡單方法(如Offline)的改進非常有限。
相比之下,Koodos顯著優於所有現有方法,彰顯出在時域泛化任務中考慮分佈連續變化的關鍵作用。
決策邊界
為直觀展示泛化效果,作者在Rotated 2-Moons數據集上進行了決策邊界的可視化。
該任務具有極高難度:模型需在0到35秒左右的35個連續時域上訓練,隨後泛化到不規律分佈在35到50秒的15個測試域。而現有方法通常只能泛化至未來的一個時域(T+1),且難以處理不規律的時間分佈。
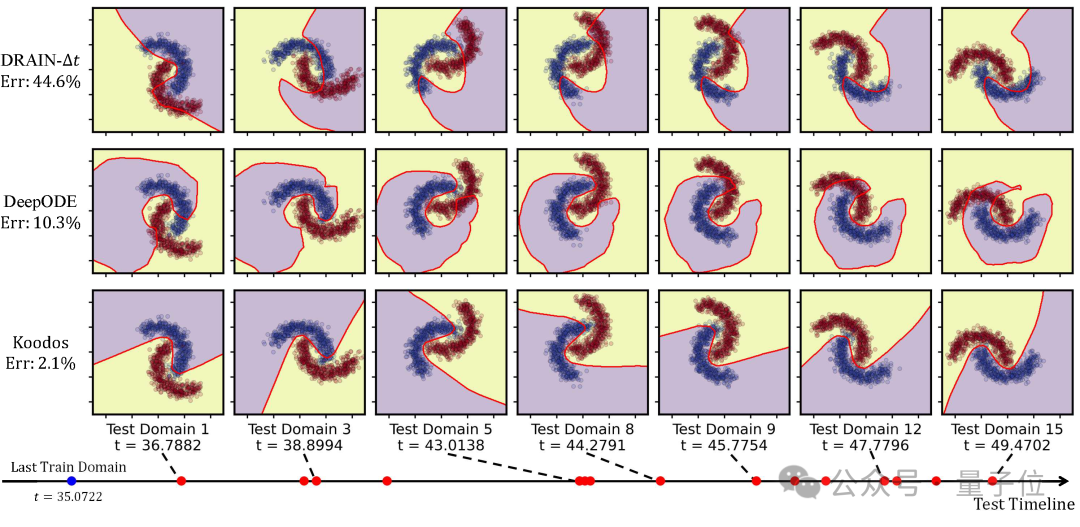
下圖展示了從15個測試域中選取了7個進行可視化測試的結果(紫色和黃色表示數據區域,紅線表示決策邊界)。
結果清晰地表明,基線方法在應對連續時域的動態變化時表現不足。隨著時間推進,決策邊界逐漸偏離理想狀態。
尤其是最新的DRAIN方法(ICLR23)在多步泛化任務中明顯失效。
相比之下,Koodos在所有測試域上展現出卓越的泛化能力,始終保持清晰、準確的決策邊界,與實際數據分佈變化高度同步。
這一效果突顯了Koodos在時域泛化任務中的優勢。
模型演變軌跡
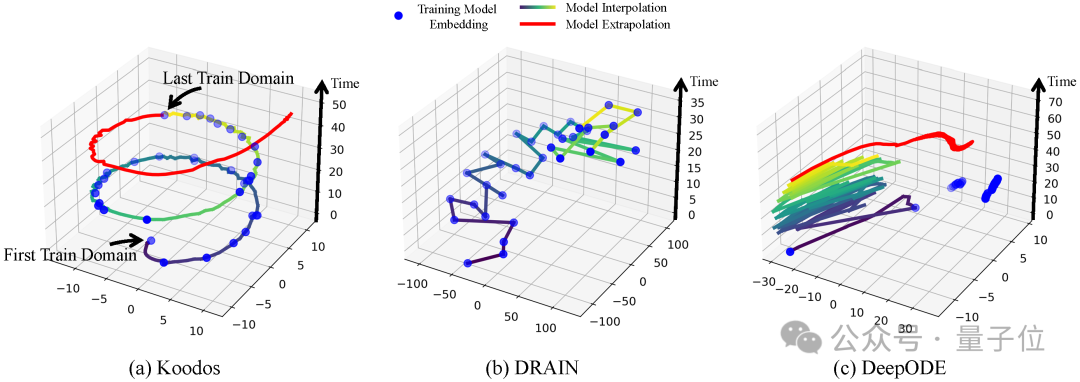
為更深入地分析模型的泛化能力,作者通過t-SNE降維,將不同方法的模型參數的演變過程(Model Evolution Trajectory)在隱空間中可視化。
可以看出,Koodos的軌跡呈現出平滑而有規律的螺旋式上升路徑,從訓練域平滑延伸至測試域。
這一軌跡表明,Koodos能夠在隱空間中有效捕捉數據分佈的連續變化,並隨時間自然地擴展泛化。
相比之下,基線模型的軌跡在隱空間中缺乏清晰結構,隨著時間推移,逐漸出現明顯的偏離,未能形成一致的動態模式。
時域泛化的分析與控制
在 Koodos 模型中,庫普曼算子為分析模型動態提供了有效手段。
作者對Koodos在2-Moons數據集上分析表明,庫普曼算子的特徵值在複平面上分佈在穩定區和不穩定區。
這意味著Koodos在中短期內能穩定泛化,但在極長時間的預測上將會逐漸失去穩定性,偏離預期路徑(下圖b)。
為提升模型的穩定性,作者通過將庫普曼算子配置為反對稱矩陣(即Koodos版本),確保所有特徵值為純虛數,使模型具有週期性穩定特性。
在這一配置下,Koodos展現出高度一致的軌跡,即使在長時間外推過程中依然保持穩定和準確,證明了引入先驗知識對增強模型穩健性的效果(下圖c)。
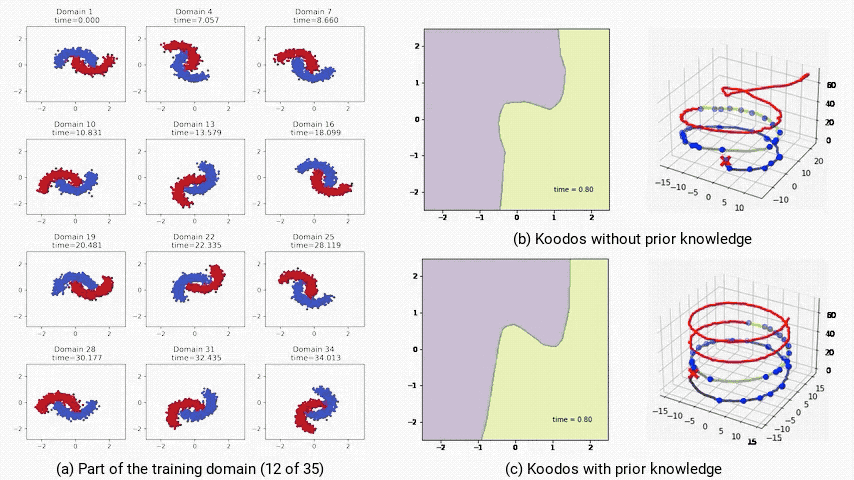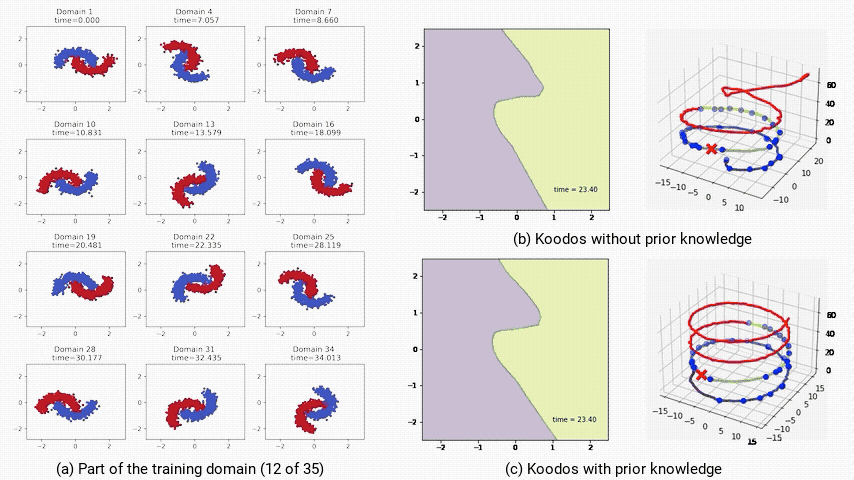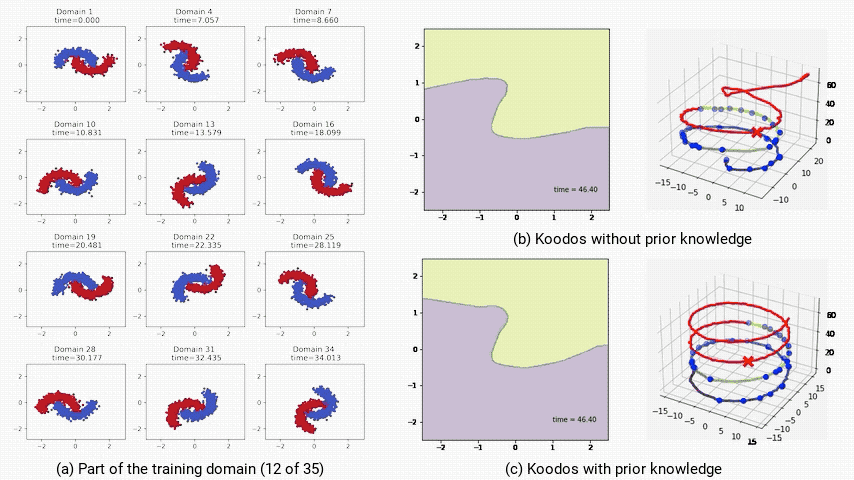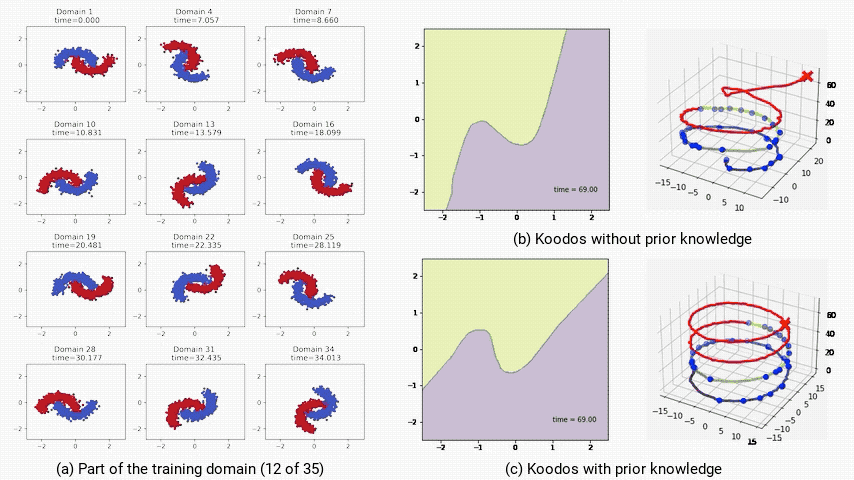 (a:部分訓練域數據;b:不受控,模型最終偏離預期;c:受控,模型始終穩定且準確。)
(a:部分訓練域數據;b:不受控,模型最終偏離預期;c:受控,模型始終穩定且準確。)時域泛化與生成式模型任務有天然的關聯,Koodos所具備的泛化能力能夠為神經網絡生成技術帶來新的可能。
Koodos的應用並不局限於時域泛化,它也可以適用於其他分佈變化的任務中。
作者計劃探索其在非時態領域的應用。
同時,作者也將探索時域泛化在大模型中的集成,幫助LLM在複雜多變的分佈中保持魯棒性和穩定性。
論文地址:
https://arxiv.org/pdf/2405.16075
GitHub:
https://github.com/Zekun-Cai/Koodos/