陶哲軒宣佈「等式理論計劃」成功，人類AI協作，57天完成2200萬+數學關係證明

魚羊 一水 發自 凹非寺

量子位 | 公眾號 QbitAI

57天，人類和AI合作搞掂了4694個等式之間22028942個蘊含關係！

大神陶哲軒激動宣佈：等式理論計劃，成功。

「等式理論計劃」，由陶哲軒本人在2024年9月25日發起，目的是探索按蘊含關係排序的原群（magma）等式理論空間。

特別的是，在這個項目里，陶哲軒不僅集合了人類數學家的力量，還把AI工具納入了合作者的範圍，包括ChatGPT、Claude和GitHub Copilot。

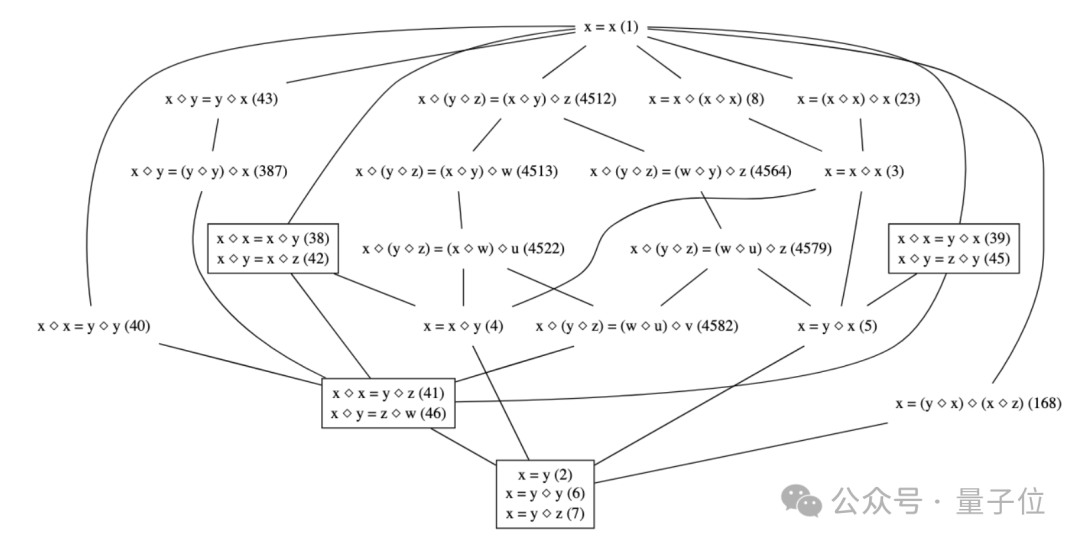
項目發起當日就正式啟動，僅僅9天，項目進度就達到了99.866%。

而現在，在2200萬+個需要證明的蘊含關係中，8178279個已被證實，13855193個已被證偽，僅有162個還懸而未決。

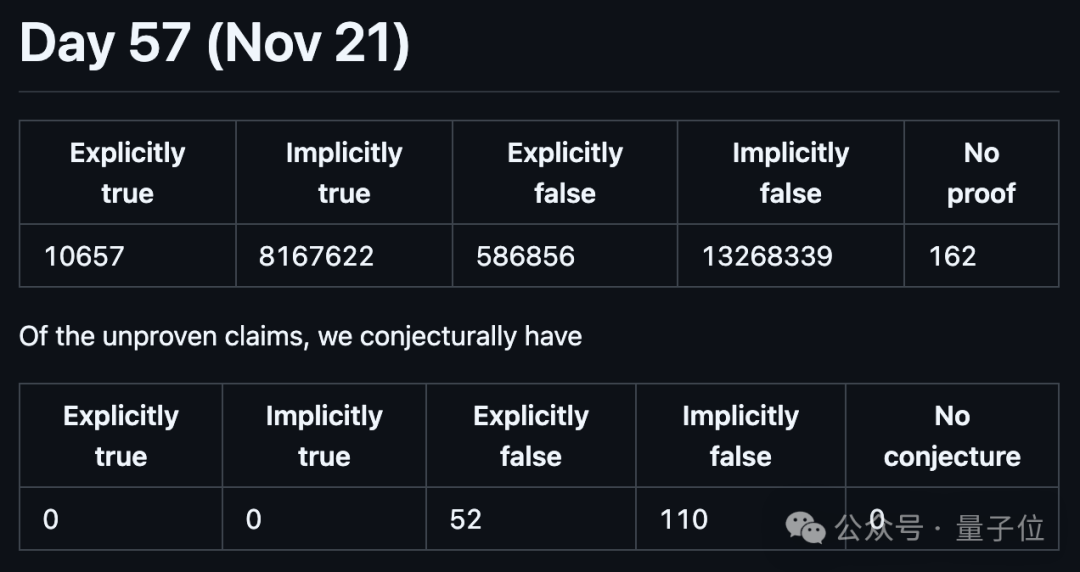
按陶哲軒的說法，就是離「宣佈完全成功」基本只是「時間問題」：

因此，我們現在已經開始著手撰寫論文了。

什麼是「等式理論計劃」

還是先來扒一扒陶哲軒這回究竟是整了個什麼樣的活兒。

簡單說，「等式理論計劃」是指：

採用」數學家+AI（包括自動定理證明系統和大模型）+證明輔助語言Lean」這樣的協作方式，構建一個展示4694個magma等式（最多四次使用magma操作）之間所有蘊含關係的 「蘊含圖」。

首先，這個計劃的最初靈感源於陶哲軒本人對「去中心化」研究方式的暢想。

傳統上，大部分數學研究項目都由少數專業數學家（通常1~5名）進行，每個人都對自己的部分更專業，且彼此可以相互驗證。

不過也是因為存在驗證環節，組織更大規模的數學項目（尤其是需要涉及公眾貢獻），一直具有挑戰性。

而現在，通過AI工具以及Lean這樣的證明輔助語言，數學項目的大規模協作變得可能。

打前陣的就有開源社區尋找美臣素數的成功嘗試，在這個代號GIMPS的誌願項目中，任何擁有強大PC或GPU的人都可以加入尋找美臣素數。

雖然證明助手這樣的AI工具在這個項目里用得還不多，但表達的精神是類似的。

因此，在開展等式理論計劃之前，陶哲軒就打算搞一個實驗：

在一個數學項目中，聚齊專業/業餘數學家、AI工具、證明輔助語言Lean等，一同幹大事！

受去年MathOverflow上一個等式問題的啟發，這一次，陶哲軒將目光瞄準了代數領域中的magma。

當時的問題是醬嬸兒的：

交換恒等式和常量恒等式之間是否存在等價關係？

拋開具體問題不談，這裏主要想說明magma涉及等式之間的關係。

簡單來說，magma是一個代數結構，它由一個集合和一個在該集合上定義的二元運算組成，但不要求滿足任何額外的代數性質，如結合律、交換律等。

我們常見的有關magma的等式包括：

而等式理論計劃，就是要找出magma中不同等式之間的等價、推出和非推出關係。

就拿上面這11個等式來看，最終的關係圖be like：

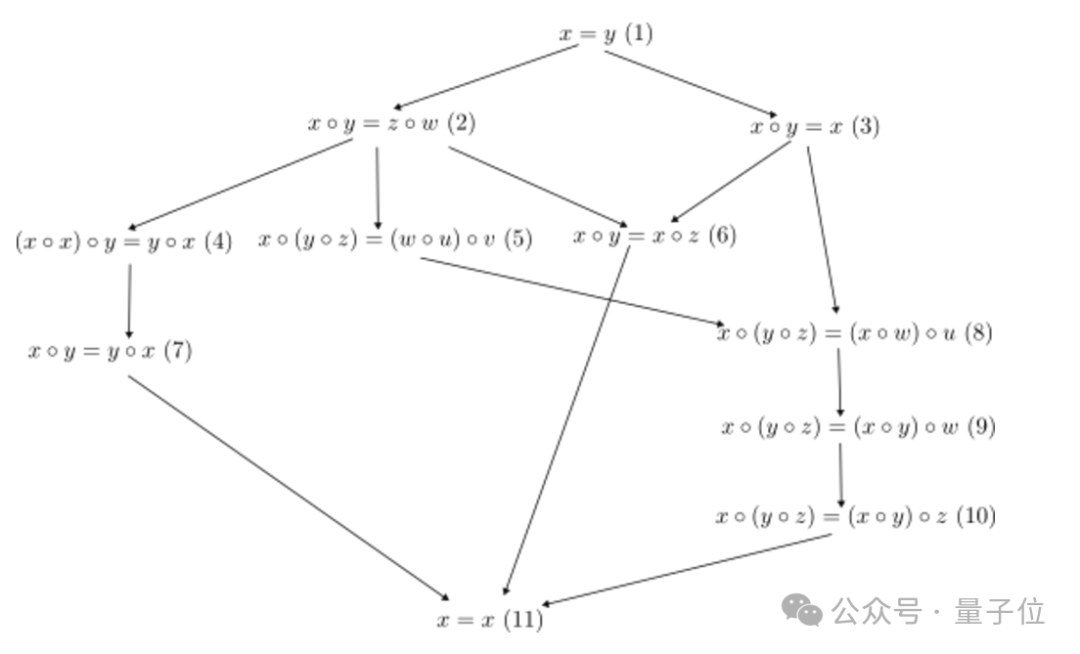
可以看出，常量公理等式（1）蘊含了其他所有等式，即如果1成立，那麼其他等式也自動成立；而反身公理等式（11）由於最寬鬆（x=x），幾乎所有的magma都滿足這個公理。

回到計劃本身，陶哲軒等人在初始階段集中研究了那些只包含一個方程的magma定律，這些方程最多包含四個magma操作（即二元運算）。

舉個例子，如果我們有一個magma（M，∗），其中M是元素的集合，∗是定義在M上的二元運算。

則一個「最多四次使用magma操作」的表達式如下：

• a∗b（一次操作）

• (𝑎∗𝑏)∗𝑐(a∗b)∗c（兩次操作）

• 𝑎∗(𝑏∗(𝑐∗𝑑))a∗(b∗(c∗d))（三次操作）

• ((𝑎∗𝑏)∗𝑐)∗(𝑑∗𝑒)((a∗b)∗c)∗(d∗e)（四次操作）

其中𝑎,𝑏,𝑐,𝑑,𝑒都是集合M中的元素，每次∗的使用都算作一次magma操作。

這樣的等式定律有4694個，由於每個定律都可能蘊含其他4693個定律（一個定律不能蘊含自身），因此總共有4694*(4694-1) = 22,028,942個可能的蘊含關係需要被證明或反駁。

這裏的蘊含關係包括「蘊含」和「反蘊含」，其中「蘊含」關係又涉及到兩種類型：

• 已證明的蘊含：在Lean中已經過驗證

• 推測的蘊含：尚未在Lean中驗證，可能由人或計算機生成

更多項目細節，陶哲軒在項目日誌中，留下了非常詳細的記錄——

9天進度99.866%，大模型有用但「表現低於預期」

簡單總結「等式理論計劃」的進度，就是一個字：快。

陶哲軒本人都說：

這個項目的進度遠超我的預期。

有多快？

僅僅48小時，很大一部分蘊含關係就已「解決在望」。

項目啟動第5天，項目參與者們已經從最初的約2200萬條蘊含關係中解決了大量簡單蘊含，只剩下約300萬的數量尚待解決。

項目啟動第9天，隨著首次重大重構的完成——合作者們改進了magma的運算符號，以使Lean代碼的編譯速度顯著加快，以及一些研究問題的推進，項目完成度一舉從87%躍升到了99.866%。

第19天，項目進度來到99.9963%。陶哲軒在他的博客文章中提及，寫論文的事已經提上日程，並且可能包含數十名作者。

GitHub顯示該項目有45位貢獻者：

到了11月21日，也就是項目第57天，隨著主項目最後一個未解決的蘊含關係被搞掂（待驗證），「等式理論計劃」目標已宣告達成。

論文可以正式開寫了。

陶哲軒透露，論文的框架早已擬好，但後續還需要大量工作來對其進行更新，並轉換為可以提交的形式。

日誌中也詳細談到了大模型工具發揮的作用。

在第一天，陶哲軒就對GitHub Copilot大加讚賞：

GitHub Copilot在處理日常任務時非常有用，比如輸入需要證明的新Lean定理，或者更新藍圖來整合最新的PR結果。

他具體舉了個例子：要將Lean轉換為LaTeX，把Lean代碼黏貼為註釋，開始敲LaTeX，GitHub Copilot就會自動補全剩下的內容。

不過，陶哲軒也坦率表示，大模型們在項目中的表現「低於預期」，更多的時候，數學家們用到的還是「經典AI」，比如自動定理證明器Vampire等。

他還提到：

項目的參與者非常多元化，包括處在職業生涯各個階段的數學家和計算機科學家，學生和業餘愛好者。Lean在整合人類和機器生成的貢獻方面表現出色。機器生成的部分在數量上是貢獻的最主要來源，不過，許多自動生成的結果最初是人類在特殊情況下得出的，之後被進一步推廣和形式化。

具體到項目中，GitHub Copilot的主要作用還是加快代碼的編寫，而Claude則被用來幫忙創建可視化工具，比如這個「等式瀏覽器」：

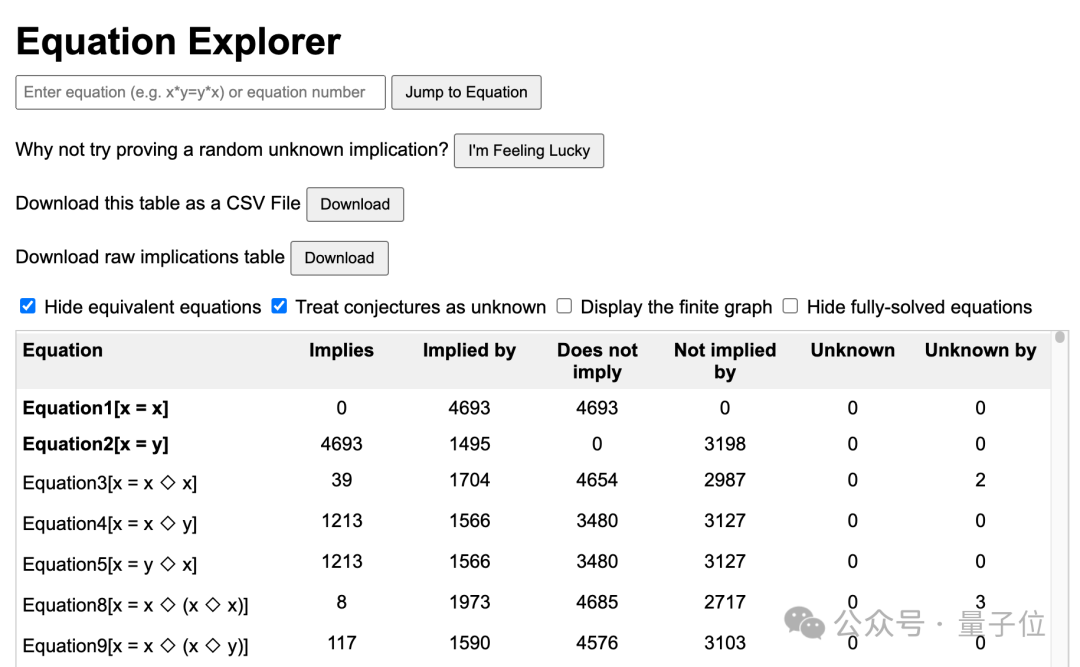
ChatGPT則更多扮演激發數學家們靈感的小助手角色。

對陶哲軒來說，ChatGPT能幫他快速掌握通用代數的一些細節。

而lyphyser、Daniel Weber、Fan Zheng和Bhavik Mehta這幾位項目參與者，還通過跟ChatGPT的討論，證明1659這個等式可能具有非平凡的合流性。

主項目里程碑達成，不過「等式理論計劃」的其他衍生項目仍在進行中，比如研究在有限原群限制下的類似蘊含圖、對蘊含圖進行數據分析等等。

陶哲軒也再次強調了這一項目和AI的聯繫：

希望項目中的蘊含關係能夠作為未來AI數學工具的基準測試。

除了陶哲軒之外，項目的主要維護人還有意大利數學家Pietro Monticone和Shreyas Srinivas。

兩位都是Lean重度愛好者。

Shreyas Srinivas主頁

Pietro Monticone還和他特倫託大學的同事們一起搞過指數3的費馬大定理的Lean版證明。

GitHub：

https://github.com/teorth/equational_theories

參考鏈接：

[1]https://mathstodon.xyz/@tao/113522452070896956

[2]https://teorth.github.io/equational_theories/

[3]https://terrytao.wordpress.com/2024/10/12/the-equational-theories-project-a-brief-tour/