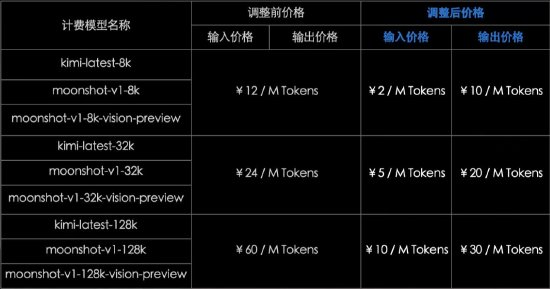
三名高中生，為近百年的分形定理帶來了新證明

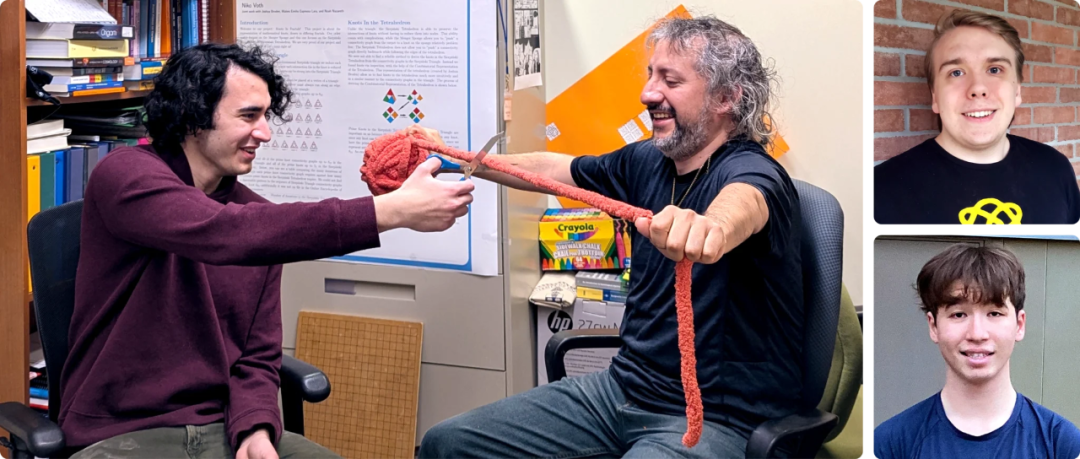
本週，量子雜誌又介紹了另一個早早就在數學領域展露頭角的三人高中生團隊：Niko Voth（右上）、Joshua Broden（右下）和 Noah Nazareth（最左）。

在他們的導師、多倫多大學數學家 Malors Espinosa（以下簡稱 Malors） 的幫助下，他們證明了一條關於扭結和分形（knots and fractals）的新定理。

2021 年秋天，Malors 開始設計一個特殊的數學問題。與任何好的研究問題一樣，這個數學問題必鬚髮人深省，解決方案也要非同尋常。當時還是多倫多大學數學研究生的他希望高中生能夠證明這個數學問題。

多年來，Malors 一直在為當地的高中生舉辦暑期講習班，教他們數學研究的基本思想，並向他們展示如何寫證明。不過，他的一些學生似乎準備做更多，他們想要找出在沒有答案的情況下做數學意味著什麼。因此，這些學生需要正確的問題來指導。

後來，Malors 在閱讀一本關於混沌的教科書時終於找到了這樣的問題。在書中，他發現了一個熟悉的物體：分形或自相似形狀，學名為門格海綿（Menger sponge），它的結構簡單但優雅。

首先將立方體分成類似魔方的形狀，接下來移除正中央的立方體以及六個面的中心立方體，最後對剩下的 20 個立方體重覆此過程。你很快就會明白為什麼得到的分形被稱為海綿：隨著每次迭代，其孔隙會成倍增加。

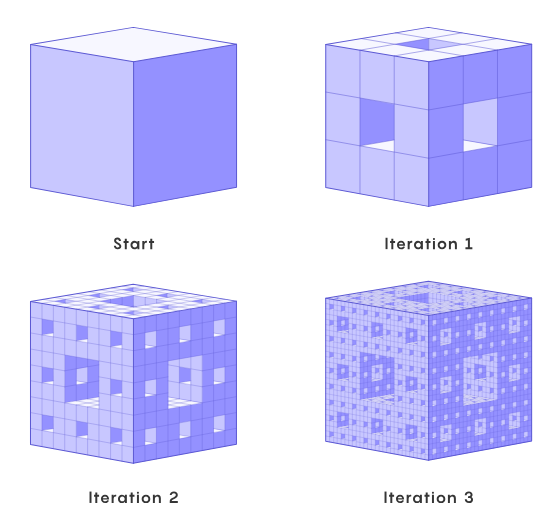
選擇門格海綿作為高中生數學「試煉場」

自從數學家 Karl Menger（卡爾・門格爾）在近一個世紀前提出分形海綿以來，它就一直吸引著專業和業餘數學家發揮想像力，原因之一是它看起來很酷。

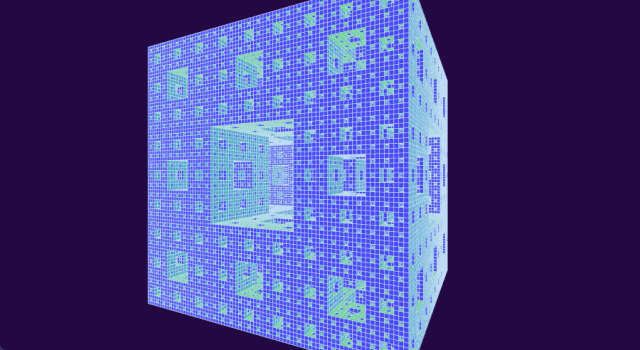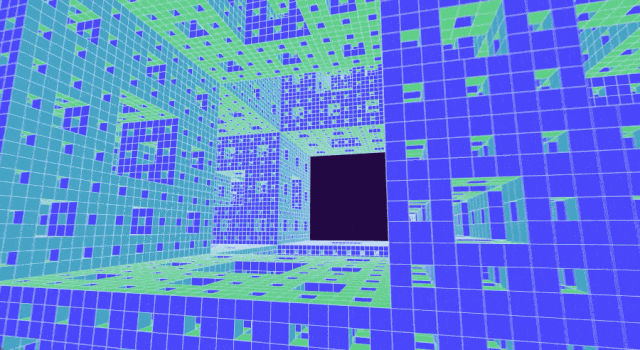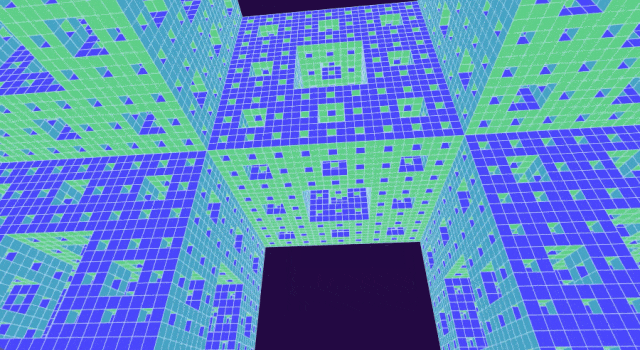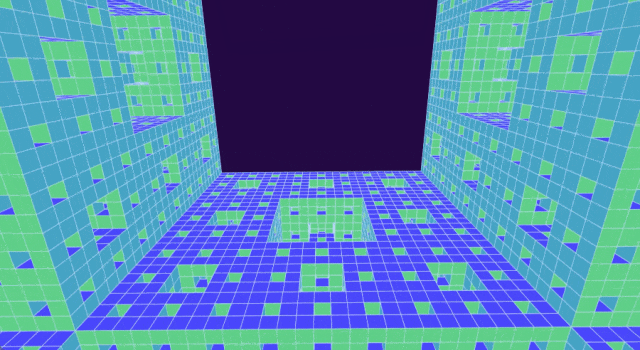
通過從起始立方體中移除越來越小的立方體，可以構造出門格海綿。

2014 年，數百名數學愛好者參加了一項名為「MegaMenger」的全球性活動，用名片製作了重達 200 磅的海綿。由於其多孔的泡沫狀結構，海綿還被用來模擬減震器和奇特的時空體形式。

最重要的是，分形具有各種違反直覺的數學特性。例如繼續拔出更小的碎片，最初的立方體就會變成完全不同的東西。經過無數次迭代後，體積會縮小到零，而其表面積會無限大。這就是分形的奇特之處：徘徊在維度之間，佔據空間但又沒有真正填滿它。

1926 年，Menger 首次定義了海綿，還證明了任何可想像的曲線（包括簡單的線條和圓圈、看起來像樹或雪花的結構、分形粉塵）都可以變形，然後嵌入海綿的某個地方。它們可以沿著海綿纏繞的輪廓蜿蜒前行，而不會離開海綿表面，不會撞到洞，也不會相互交叉。Menger 寫道，「這種海綿是一條通用曲線。」

但 Malors 後來意識到，這又引出了一個新問題。Menger 雖然已經證明，你可以在海綿中找到一個圓。但在某種意義上，與圓等價的物體又如何呢？

考慮數學上的一個扭結：一根繩子被扭成一團，然後兩端閉合形成一個環。從外面看，它可能看起來像一團亂麻。但一隻螞蟻沿著它爬，最終會回到起點，就像在圓上一樣。這樣一來，每個扭結都等價於圓，或「同胚於」圓。

每個扭結都「同胚於」圓，這意味著可以將點從一個點映射到另一個點，同時滿足一組簡單的條件。

不過，Menger 的證明沒有區分同胚曲線，他的證明僅保證可以在海綿中找到圓，而不是所有同胚扭結中都可以找到。因此，Malors 想證明可以在海綿中找到每個扭結。

這個問題似乎激發了年輕學生們的興趣，他們最近在 Malors 的研討會上學習了扭結，玩得很開心。誰不喜歡分形呢？問題在於是否可以完成自己的證明。「我真的希望有一個答案，」Malors 表示。

最終，在與 Malors 每週進行 Zoom 會議幾個月後，他的三名高中學生，即 Niko Voth、Joshua Broden 和 Noah Nazareth，證明了所有扭結確實都可以在門格海綿中找到。另外，他們還發現，另一種相關的分形也可能存在同樣的情況。

• 論文標題：Knots inside Fractals

• 論文地址：https://arxiv.org/pdf/2409.03639

對此，北卡羅來納州立大學拓撲學家 Radmila Sazdanovic 表示，這是一種巧妙的把事物組合在一起的方法。在重新審視 Menger 百年歷史的定理時，Malors 顯然提出了一個以前沒人想過要問的問題，這是一個非常新穎的想法。而且，他的三名學生完成了證明。

從另一個角度思考扭結

多年來，Broden、Nazareth 和 Voth 參加了 Malors 的幾次夏季研討會。在早期的研討會上，當 Malors 第一次教他們扭結時，14 歲的 Voth 被深深震撼了。

然而，他們遇到了一些極其複雜的 Menger 問題，這與他們以前的作業不同，沒有現成的答案可以參考。 

Nazareth 表示這個問題讓他感到緊張，因為這是他第一次做沒人知道答案的事情，連 Malors 也不知道。「也許根本就沒有答案。」

他們的目標就像是要將一根顯微針穿過一團塵土，這團塵土是海綿在多次移除材料後的殘餘物。這項任務極度複雜，他們需要把針插到正確的地方，打結的過程必須極為精準，不能出錯，也不能偏離原本的結構。任何一個扭結如果線漂浮在海綿的空洞里，就意味著失敗。 

這不是一件容易的事。但有一種方法可以簡化它。扭結可以在一張平整的紙上以稱為弧表示（arc presentation）的特殊圖表來描繪。要創建一個扭結，首先要瞭解扭結的線如何在彼此前面或後面穿過。然後應用一組規則將這些信息轉換為網格上的一系列點。網格的每一行和每一列都將包含兩個點。

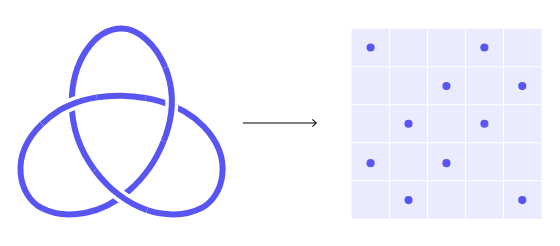
用水平線和垂直線連接這些點。當兩條線段相交時，將垂直線段畫在水平線段前面。

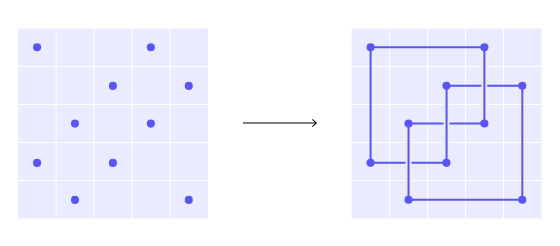
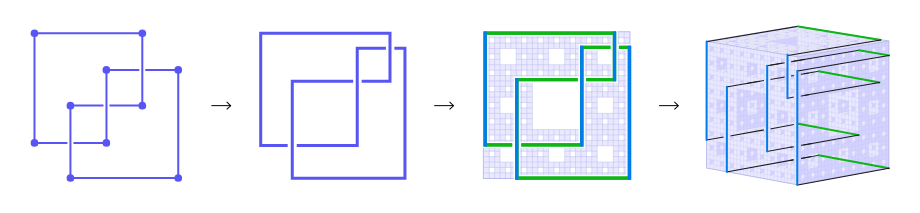
每個結都可以用這種網格狀的方式表示。當學生們考慮交叉線段的圖形時，他們想到了門格海綿的表面。將弧表示的水平線放置在海綿的一面，將垂直線放置在相反的一面，這就足夠簡單了。

難點在於如何連接這個扭結 —— 如何將其拉伸回三維空間。

數學家們轉向了所謂的康托爾集，構造這個集的步驟是：從一個線段開始，將其分成三等份，去掉中間的三分之一，然後對剩下的兩個部分重覆相同的操作，依此類推，直到無限進行下去。最終，你將只剩下一些散落的點。 

康托爾集和門格海綿的結構有相似之處，都是通過去除中間部分或某些區域逐漸構建出來的。他們意識到，當海綿的面上的點的坐標都在康托爾集中的時候，這些點的位置上不應該有空洞。更重要的是，由於海綿具有重覆的設計結構，這些點背後的位置也不應該有空洞。因此，扭結可以在海綿的結構中自由地穿過，而不會不小心脫離海綿的物質。 

那麼，剩下的就是讓學生證明他們總是可以壓縮或拉伸給定扭結的弧表示，以便其所有角都與康托爾集合中的坐標對齊。

為了完成最後一步，Broden、Nazareth 和 Voth 採取了一個捷徑。他們證明了可以變形任何弧線表示法，使得其垂直和水平線段交叉的點都位於康托爾集中。他們可以始終將一個給定的扭結嵌入門格海綿的某一迭代中。 

現在他們已經解答了 Malors 原本的問題，他們還想更進一步。他們已經開始研究是否所有扭結都可以嵌入到四面體版本的門格海綿中：

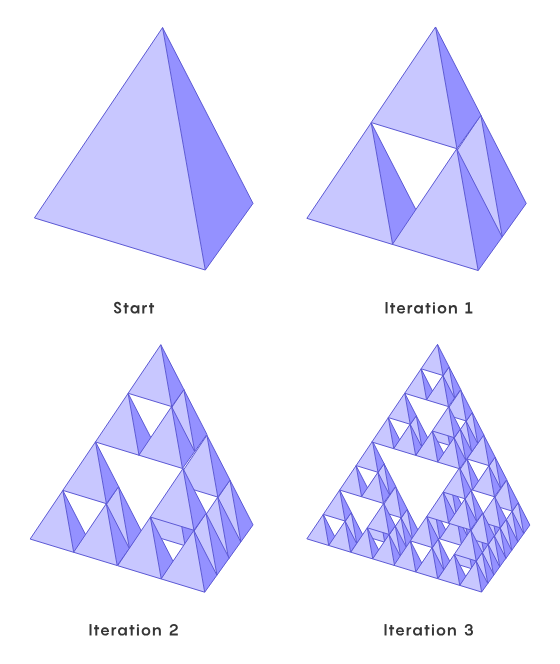
Broden 說：「這讓人非常惱火。」如果沒有將這些面直接對齊，他們將扭結穿過該分形的方法就不再有效。

扭結度量

Malors 表示，正是在這個階段，學生們瞭解到了數學研究的痛苦 —— 數學的很大一部分工作內容都是尋找有希望的前進之路，然後遭遇失敗。「我們面對的是數學，而數學並不憐憫任何人。」他說 ，「不過對於高中生來說，通常還不會受到這種傷害。」

Malors 之前以為不可能在四面體中找到所謂的三葉結。在一次影片通話中，這三名學生反駁了這一觀點。他們回憶說，離開會議時感到沮喪和失望。但他們決定堅持自己的直覺。

幾週後，令 Malors 驚訝的是，他們帶著一個結果回來了：他們找到了一種新方法，可將三葉結的弧表示映射到四面體上。之後他們證明，所有「扭結麵包（pretzel）」形式的扭結都能做到這一點（三葉結也屬於此類別），但對於其他類型的扭結而言，這個問題仍未得到解決。

各種扭結麵包，圖源：域奇百科

Malors 推測，這些學生的方法也許能提供更廣泛適用的測量分形複雜性的方法。並非所有分形都允許各種扭結。也許可以根據它們可以容納和不能容納的扭結類型來更好地理解它們的結構。

至少，這項研究能啟發新的藝術成果，類似於 2014 年的 MegaMenger 競賽。維珍尼亞聯邦大學的扭結 結理論科學家 Allison Moore 說：「看到它被用物理材料建造出來真是太好了。」

與此同時，Joshua Broden、Noah Nazareth 和 Niko Voth 全都已經高中畢業。僅有 Joshua Broden 決定繼續研究四面體問題（當他不忙於大學課程時），但他們三個人都在考慮從事數學研究工作。

Nazareth 說：「如果能為比自己更偉大的事情、為真理做出貢獻，會感覺很有意義。」而這一切的起點是問出那個正確的問題。

原文鏈接：https://www.quantamagazine.org/teen-mathematicians-tie-knots-through-a-mind-blowing-fractal-20241126/