DeepMind用語言遊戲讓大模型學AlphaGo自我博弈，數據限制不存在了

機器之心報導

編輯：澤南、蛋醬

自我博弈，很神奇吧？

我們終於朝著真正自主、自我完善的人工智能邁出了重要一步？

上週末，一篇 Google DeepMind 的論文引發了 AI 圈的關注。研究者引入了「蘇格拉底式學習」，這是 AI 中遞歸自我完善的一種新方法。這種方法使系統能夠自主增強其能力，超越初始訓練數據的限制。通過利用結構化的「語言遊戲」，該技術可以為實現通用人工智能提供了實用的路線圖。

在該工作中，DeepMind 提出的框架圍繞封閉、自給自足的環境，AI 系統無需外部數據即可運行。要實現目標，智能體必須滿足三個關鍵條件：反饋與目標一致，廣泛的數據覆蓋範圍，以及足夠的計算資源。這種設計促進了獨立學習，為通向 AGI 提供了一條可擴展的途徑，同時解決了數據生成和反饋質量等挑戰。

新方法的核心是進行「語言遊戲」，即智能體之間結構化的交互、解決問題並以分數的形式接收反饋。這些遊戲允許人工智能進行自我博弈，生成數據並完善技能，也無需人工輸入。遞歸結構使系統能夠自主創建和開局新遊戲，解鎖更抽像的解決問題的能力並擴展其能力。

最終的創新在於 AI 自我改造，智能體不僅可以從環境中學習，還可以重新配置其內部系統。這樣可以消除固定架構帶來的限制，為超過以往的性能改進奠定基礎。總之，DeepMind 的研究強調了蘇格拉底式學習作為創造真正自主、自我完善的人工智能的變革性步驟的潛力。

讓我們看看這篇論文是怎麼說的：

• 論文標題：Boundless Socratic Learning with Language Games

• 論文鏈接：https://arxiv.org/abs/2411.16905

考慮一個隨時間演變的封閉系統（無輸入、無輸出）（見圖 1）。系統內有一個具有輸入和輸出的實體，稱為智能體（Agent），它也會隨時間發生變化。系統外部有一個觀察者，其目的是評估智能體的性能。如果性能不斷提高，我們就把這對系統和觀察者稱為改進過程。

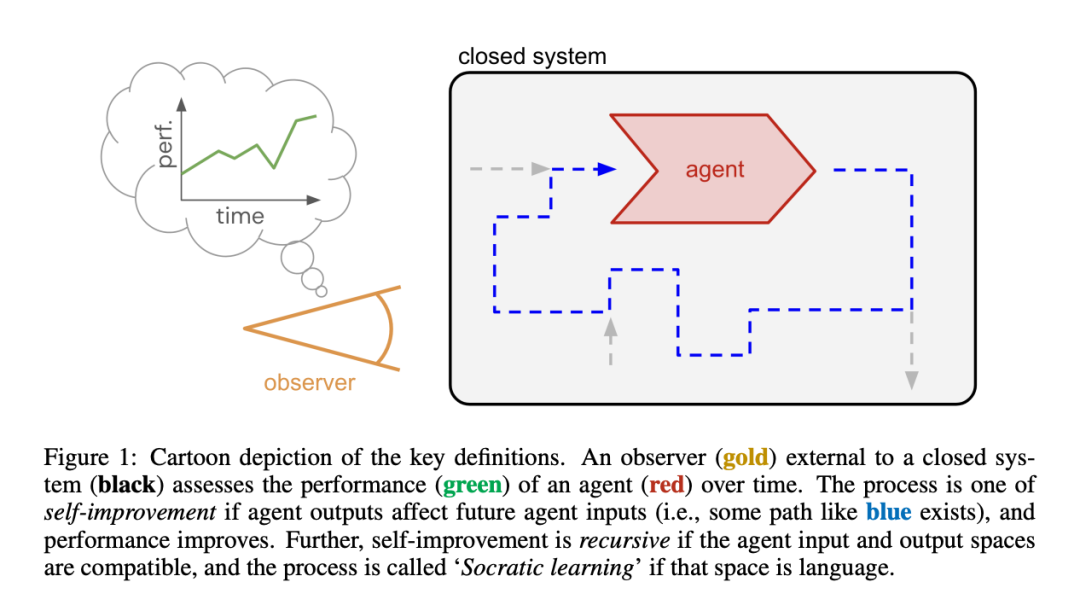
這一過程的動態變化由智能體及其周圍系統共同驅動，但為了使評估定義明確，需要設定明確的邊界：事實上，智能體就是可以明確評估的對象。同樣，為了分離關注點，觀察者被刻意置於系統之外：由於系統是封閉的，觀察者的評估無法反饋到系統中。因此，智能體的學習反饋必須來自系統內部的智能體，如損失、獎勵函數、偏好數據或批評者。

在這裏，最簡單的性能指標是一個標量分數，可以在有限的時間內測量，也就是在（一系列）偶發任務中測量。從機制上講，觀察者可以通過兩種方式來衡量性能，一是被動地觀察智能體在系統中的行為（如果所有相關任務都是自然發生的），二是通過複製和探測評估，即讓智能體的複製副本面對自己選擇的交互任務。

在不失通用性的前提下，智能體內部的元素可分為三類：固定元素不受學習的影響，例如它的底層或不可修改的代碼；瞬態元素不會在不同事件之間或不同評估之間延續（如激活、隨機數生成器的狀態）；最後，學習元素（如權重、參數、知識）會根據反饋信號發生變化，它們的演變會映射出性能差異。

可以通過隱含的生命週期來區分改進過程；有些改進過程是開放式的，可以無限制地持續改進，而有些改進過程則會在某個有限時間後收斂到其漸進性能。

自我完善的三個必要條件

DeepMind 研究者認為，自我完善是一種改進過程，但附加標準是智能體自身的輸出（行動）會影響其未來的學習。換句話說，智能體在系統中塑造（部分）自己的經驗流，有可能在封閉系統中實現無限的改進。這種設置對於強化學習社區（RL）的讀者來說可能很熟悉：RL 智能體的行為會改變其學習的數據分佈，進而影響其行為策略。

自我完善過程的另一個典型實例是自我對弈，其中系統（通常稱遊戲）將智能體置於玩家和對手的角色中，以生成帶有反饋（誰贏了）的無限經驗流，為不斷增加的技能學習提供方向。從它與 RL 的聯繫中，我們可以得出自我完善發揮作用的必要條件，並幫助澄清有關係統的一些假設。前兩個條件，反饋和覆蓋度是原則上的可行性，第三個條件規模是實踐上的可行性。

研究者考慮的自我完善過程的具體類型是遞歸自我完善，其中智能體的輸入和輸出是兼容的（即存在於同一空間中），並且輸出成為未來的輸入。與輸出僅影響輸入分佈的一般情況相比，這更具限制性，但中立性更低，最常見的實例是將智能體輸出映射到輸入的（複雜）環境。這種類型的遞歸是許多開放式過程的屬性，開放式改進可以說是 ASI 的核心特徵。

這種兼容的輸入和輸出空間的一個極好的例子就是語言。人類的大量行為都是通過語言來介導和表達的，尤其是在認知領域（從定義上講，認知領域是 ASI 的一部分）。正如查馬斯 (2024) 和他之前幾個世紀的理性主義者所言，語言可能足以進行思考和理解，而不需要感官基礎。語言又同時具有抽像的巧妙特性，可以在共享空間中編碼概念層次結構的多個級別。

在文章的其餘部分，研究者使用「蘇格拉底式學習」來指代在語言空間中運作的遞歸式自我完善過程。這個名字暗示了蘇格拉底通過質疑對話和反復的語言互動來尋找或提煉知識的方法。但值得注意的是，這種方法並不是去收集現實世界中的觀察結果 —— 這反映了系統強調的封閉性。

蘇格拉底式學習的本質局限性

在自我完善的三個必要條件中，覆蓋和反饋這兩個條件原則上適用於蘇格拉底式學習，而且仍然是不可還原的。為了儘可能清楚地說明這兩個條件的含義，本節中忽略了第三個條件（規模、實用性和效率問題），而從長遠的角度來考慮這種簡化的動機：如果計算能力和內存繼續呈指數增長，那麼規模限制只是暫時的障礙。如果不是這樣，考慮蘇格拉底式學習的資源受限情景（類似於研究有界理性）仍能產生有效的洞察。

覆蓋條件意味著蘇格拉底學習系統必須不斷生成（語言）數據，同時隨著時間的推移保持或擴大多樣性。在 LLM 時代，這似乎並不太牽強：我們可以設想，一個生成智能體初始化時擁有類似互聯網的廣泛分佈，它可以生成永無止境的新語言表達流。然而，在遞歸過程中防止生成分佈的漂移、崩潰或縮小可能非常困難。

反饋條件要求系統：（a）持續產生關於智能體輸出（某些子集）的反饋，這在結構上要求批評者能夠評估語言，（b）反饋與觀察者的評估指標保持足夠一致。這造成挑戰的原因有很多：語言空間中定義明確、有依據的衡量標準往往局限於狹隘的任務，而人工智能反饋等通用性更強的機制則可以加以利用，尤其是在允許輸入分佈發生變化的情況下。

例如，目前的 LLM 訓練範式都沒有足以滿足蘇格拉底式學習的反饋機制。下一個 token 的預測損失是有依據的，但與下遊的使用情況不夠一致，而且無法推斷出訓練數據之外的情況。根據定義，人類的偏好是一致的，但卻阻礙了在封閉系統中的學習。將這種偏好緩存到已學習的獎勵模型中會使其自成一體，但從長遠來看會被利用並可能出現錯位，而且對分佈外數據的影響也很微弱。

換句話說，純粹的蘇格拉底式學習是可能的，但它需要廣泛的數據生成和強大且一致的批評能力。然而，當這些條件都具備時，其潛在改進的上限就會受到應用資源量的限制。目前已有的研究還沒有為此製定出成功的方法，接下來的內容會就如何進行蘇格拉底式學習提出一個具體但相當籠統的建議。

「Language games are all you need」

在該研究中，研究者認為 AI 的訓練可以借鑒維特根史丹的語言遊戲概念。在其中，並不是讓詞語捕捉意義，而是讓語言的互動性做到這一點。具體來說，語言遊戲定義為一種互動協議（一組規則，可以用代碼表達），它指定了一個或多個具有語言輸入和語言輸出的智能體（「玩家」）之間的互動，以及遊戲結束時每個玩家的標量評分函數。

如此定義的語言遊戲滿足了蘇格拉底式學習的兩個主要需求。即，1）它們為無限制的交互式數據生成和自我博弈提供了一種可擴展的機制，2 同時自動提供伴隨的反饋信號（分數）。

事實上，它們是覆蓋和反饋條件的邏輯結果，幾乎一直在被應用。如果將這個過程視為遊戲過程，我們就立即可以意識到多智能體動態產生的豐富策略具有很大潛力。

另外，許多常見的 LLM 交互範式也可以被很好地表示為語言遊戲，例如辯論、角色扮演、心智理論、談判、越獄攻防，或在封閉系統之外，來自人類反饋的 RL 等範式 (RLHF)。

回到哲學家：我們能想像他們玩上幾千年的語言遊戲嗎？相反，也許他們在玩多種語言遊戲時更有可能擺脫狹隘的結果。維特根史丹（又是他）也提出過同樣的觀點：他堅決反對語言具有單一的本質或功能。使用許多狹義但定義明確的語言遊戲而不是單一的通用遊戲，可以解決一個關鍵的兩難問題：對於每個狹義遊戲，都可以設計出可靠的得分函數（或批評家），而正確地獲得單一的通用函數則更加難以捉摸（即使原則上是可能的，正如 Silver 等人所論證的那樣）。從這個角度看，蘇格拉底式學習的整個過程就是一個元遊戲，它安排了智能體玩的語言遊戲並從中學習（根據 Carse (2011)，這是一個「無限」遊戲）。

研究者認為，原則上這一想法足以解決覆蓋問題。具體來說，如果有觀察者感興趣的分佈的智能體（例如，任務的驗證集），就可以用來驅動元遊戲中的探索。

正如蘇格拉底本人的經歷，蘇格拉底式的思考過程並不能保證與外部觀察者的意圖保持一致。語言遊戲作為一種機制，也沒有迴避這一點，但可以說，它降低了所需的精確度：我們所需要的不是一個在單個輸入和輸出的細粒度上保持一致的批評家，而是一個能夠判斷哪些遊戲應該玩的「元批評家」：也許沒有一個語言遊戲是完全一致的，但可以做的是，根據它們是否（在玩和學習時）做出了總體上積極的淨貢獻，對眾多遊戲進行篩選。

此外，一個遊戲的有用性並不需要事先評估，而是可以在玩過一段時間之後進行事後判斷。與此相關，一個有益的不對稱現像是，事後發現偏差的突發行為可能比設計遊戲防止這種行為要容易得多。所有這些特性都是結構上的寬鬆形式，賦予了語言遊戲框架巨大的擴展潛力。暫時跳出此處對封閉系統的假設：當我們實際構建人工智能時，我們幾乎肯定不會樂觀地相信對齊會得到保持，而是會儘可能仔細地持續檢查這一過程，並可能在整個訓練過程中對系統進行干預和調整。

在這種情況下，明確地將遊戲分佈（伴隨著可解釋的遊戲描述和每個遊戲的學習曲線）作為旋鈕提供給設計者，可能是一種有用的抽像方法。

更高階的遞歸

到目前為止，本文討論了遞歸的最低必要形式，即一種將智能體（部分）輸出反饋給自身的循環形式。在語言遊戲的框架內，研究者還想到了另外兩種遞歸形式。第一種思路是告訴智能體它正在玩哪個遊戲，並讓它選擇切換遊戲、切換到哪個遊戲以及何時切換。

這與分層或以目標為條件的 RL 有關，為智能體提供了更多的自主權和更抽像的行動空間。在將更多責任轉移給智能體的同時，與智能體外部的硬聯線遊戲選擇過程相比，這種設置可以顯著改善結果，但當然，這種額外的自由度可能會帶來崩潰或錯位的額外風險。

其次，由於遊戲是可以完全用代碼表示的交互協議，因此它們可以存在於語言智能體的輸出空間中。一開始，它可以簡單地生成現有遊戲的局部變體，從而調整主題的難度水平，之後再對遊戲進行重組，最終實現全新生成。這導致了語言遊戲空間而非語言空間的二階覆蓋問題，需要通過過濾、優先排序或課程來解決。

這兩種遞歸擴展的結合就是一個有能力的智能體，它可以通過遊戲的生成和玩耍來玩完整的元遊戲，即如何改進自己。這種元博弈雖然優雅動人，但卻缺乏內部語言博弈的明確反饋機制，而且像學習進度這樣的既定智能體指標是否足以長期保持覆蓋和對齊特性，也是一個有待研究的問題。

遞歸的下一步，也是最後一步是遞歸自我改造，也就是說，智能體的行為會改變其自身的內部結構，而不僅僅是影響其輸入流。這些方法的特點是可以以這種方式修改哪些內容（哪些內容保持不變），以及智能體可以進行多少自省，或者說可以訪問其自身的工作原理。在極端情況下，一個完全自我反省的智能體可以觀察和修改自身的任何方面，而無需間接操作。

原則上，這種類型的智能體具有最高的能力上限；由於漸進性能受到其固定結構的限制，解凍部分結構並使其可修改只會增加上限。尤其是，總有可能將新靈活參數設置為凍結時的狀態，以恢復靈活性較低的智能體的性能（在不考慮學習動力的情況下）。

從這種角度看，過去關於如何設計自我參照系統的建議並不實用，但現代 LLM 在代碼理解和生成方面的能力正在改變競爭環境，可能很快就會將這些想法從空洞轉向關鍵。

參考內容：

https://x.com/kimmonismus/status/1862993274727793047