AI做數學學會「動腦子」,UCL等發現LLM「程序性知識」,推理絕不是背答案
LLM,究竟會不會推理?
就在剛剛,UCL、Cohere等機構的研究人員發現:在LLM執行推理任務時,竟存在著一種「程序性知識」。
 論文地址:https://arxiv.org/abs/2411.12580
論文地址:https://arxiv.org/abs/2411.12580這項工作已經登上了Hacker News的熱榜。

跟很多人想像的不同,LLM在推理時,並不是使用簡單的檢索。
真相是,LLM在推理任務中進行泛化時,依賴的是文檔中的「程序性知識」,使用可概括的策略,來綜合推理任務的解決方案。
研究發現,在涉及「世界上最長的河流」、「人體最常見的元素」這類問題時,模型所依賴的數據集並不相同。

然而一旦涉及到數學題這類推理問題,LLM卻使用了某種策略,從文檔中綜合出了一種「程序性知識」。

推理集中的示例,關於「求解線性方程中的x」
有人表示,既然LLM不可能在訓練數據中找到每一個問題的例子,那就可以認為,LLM已經在進行某種形式的推斷,以創造出對所提問題的解決方案。

更有趣的是,此前蘋果的研究者曾在一篇論文中發現,GPT-4o、o1、Llama、Phi、Gemma和Mistral等模型,都未被發現任何形式推理的證據,而更像是複雜的模式匹配器。
只要給數學題換個皮,對無關緊要的信息進行修改,LLM就不會做了。
而UCL這項工作的結果,並未和蘋果的這篇論文發生矛盾。

有人根據這項研究的結果,做出這樣的總結:LLM不適合推理,但非常適合充當一種「編譯器」層,彌合自然語言和SQ、prolog、python、lean等形式語言的差距。
再對形式語言層的結果和輸出進行綜合,這基本上就是智能體了。

有網民分析表示,這個過程並不是「學習如何解決問題」的泛化,而是更具體的:「神經網絡被訓練去模仿人類在解決特定問題時展示的逐步過程」。
也就是說,LLM是通過觀察人類程序化解決問題的示例,從而複製類似的推理。

另外還有一些網民更加犀利:「大多數人活了幾十年都搞不懂該如何正確地推理,並且經常陷入邏輯謬誤當中;現在竟然覺得自己可以評判LLM是不是具有推理能力了?」

「程序性知識」被發現了
長久以來,LLM的能力和局限性,令人著迷卻又矛盾。
一方面,LLM解決一般問題的能力十分驚豔。可另一方面,跟人類相比,它們表現出的推理缺陷又令人啼笑皆非,因此讓人懷疑:它們的泛化策略是否具有穩健性?
為了探討LLM究竟採用何種泛化策略,研究人員對LLM在執行推理任務時依賴的預訓練數據進行了研究。
在兩種不同規模的模型(7B和35B)及其25億預訓練token中,研究人員識別出哪些文檔對三種簡單數學推理任務的模型輸出產生了影響,並將其與回答事實性問題時具有影響力的數據進行了對比。
就是在這個過程中,他們發現了「程序性知識」的存在!
具體來說,雖然模型在回答每個事實性問題時依賴的數據集大多是不同的,但在同一任務中的不同推理問題上,一個文檔確往往表現出了類似的影響力。
 事實控制集的示例,類似於7B事實查詢集中關於「世界上最高的山」的問題,但不需要任何事實回憶
事實控制集的示例,類似於7B事實查詢集中關於「世界上最高的山」的問題,但不需要任何事實回憶另外他們還發現,對於事實性問題,答案通常出現在最具影響力的數據中。
然而,對於推理問題,答案通常不會出現在高度影響力的數據中,中間推理步驟的答案亦是如此。
原因為何?果然,還是和「程序性知識」有關。
對此,研究人員對推理問題的高排名文檔進行了定性分析後,確認了這些具有影響力的文檔的確通常都是包含程序性知識的,比如展示了如何使用公式或代碼求解的過程。
總之,模型在推理時並不是簡單檢索,而更像是使用一種可泛化的策略,即從進行類似推理的文檔中綜合程序性知識。
 推理控制集的示例,表明上類似於斜率查詢,但不需要任何推理
推理控制集的示例,表明上類似於斜率查詢,但不需要任何推理LLM是如何從預訓練數據中學習推理的?
LLM在推理中,是否真正理解了問題呢?
許多研究一致發現:LLM的能力,嚴重依賴於訓練數據中類似問題的頻率。
這就牽出了「數據汙染」的問題:基準數據往往會出現在預訓練數據集中。
在機器學習中,可以將測試數據與訓練數據分離來衡量泛化能力,但當前先進模型設計中使用的數萬億token,已經已無法合理地與基準測試數據完全分離了。
許多研究都表明,相當多常見的基準測試,都含有大量汙染數據。 即使是經改寫的基準數據,也可能會規避基於N-gram的檢測方法,對性能產生影響。
LLM究竟是在何種情況下,依賴汙染數據進行推理的呢?
這個問題,又引發出了另一個核心問題——LLM是如何從預訓練數據中學習推理的?
因此,在這項研究中,研究人員們重點專注的是語言模型用於泛化的預訓練數據,而非直接解釋模型的權重。
 推理集中的示例,涉及計算穿過兩點直線的斜率
推理集中的示例,涉及計算穿過兩點直線的斜率哪些數據會影響模式生成的推理過程?這些數據如何與所解決的具體問題相關?
模型是否僅僅從已見過的預訓練數據中「提取」答案並重新整合,還是在泛化中採用了一種更為穩健的策略?
為此,研究人員們借助了一種來自魯棒統計學的方法,讓它適配於大規模Transformer,以計算預訓練文檔對訓練模型中提示詞-完成對(prompt-completions pairs)概率的影響。
可以猜測,在極端情況下,回答推理問題的語言模型可能嚴重依賴於從預訓練數據的特定文檔中檢索的參數化知識。這些文檔包含所需檢索的信息(即推理軌跡),對模型的輸出貢獻顯著,相比之下,許多其他文檔的作用則微乎其微。
相反,在另一種極端情況下,模型可能從與問題更抽像相關的廣泛文檔中汲取信息,每份文檔對許多不同問題都會產生類似影響,但對最終輸出的貢獻相對較小。而泛化能力更強的推理應更類似於後一種策略。
事實是不是如此呢?
他們研究了對一組事實性問題和推理問題(稱為「查詢」)具有影響力的預訓練數據(稱為「文檔」)。
推理問題涵蓋三種數學任務:兩步算術、斜率計算和線性方程求解。
這些任務代表了逐步推理不同層次的挑戰,而事實性問題則需要從參數化知識中檢索答案。
對兩種LLM(7B和35B)及其25億預訓練token進行實驗後,他們的發現如下——
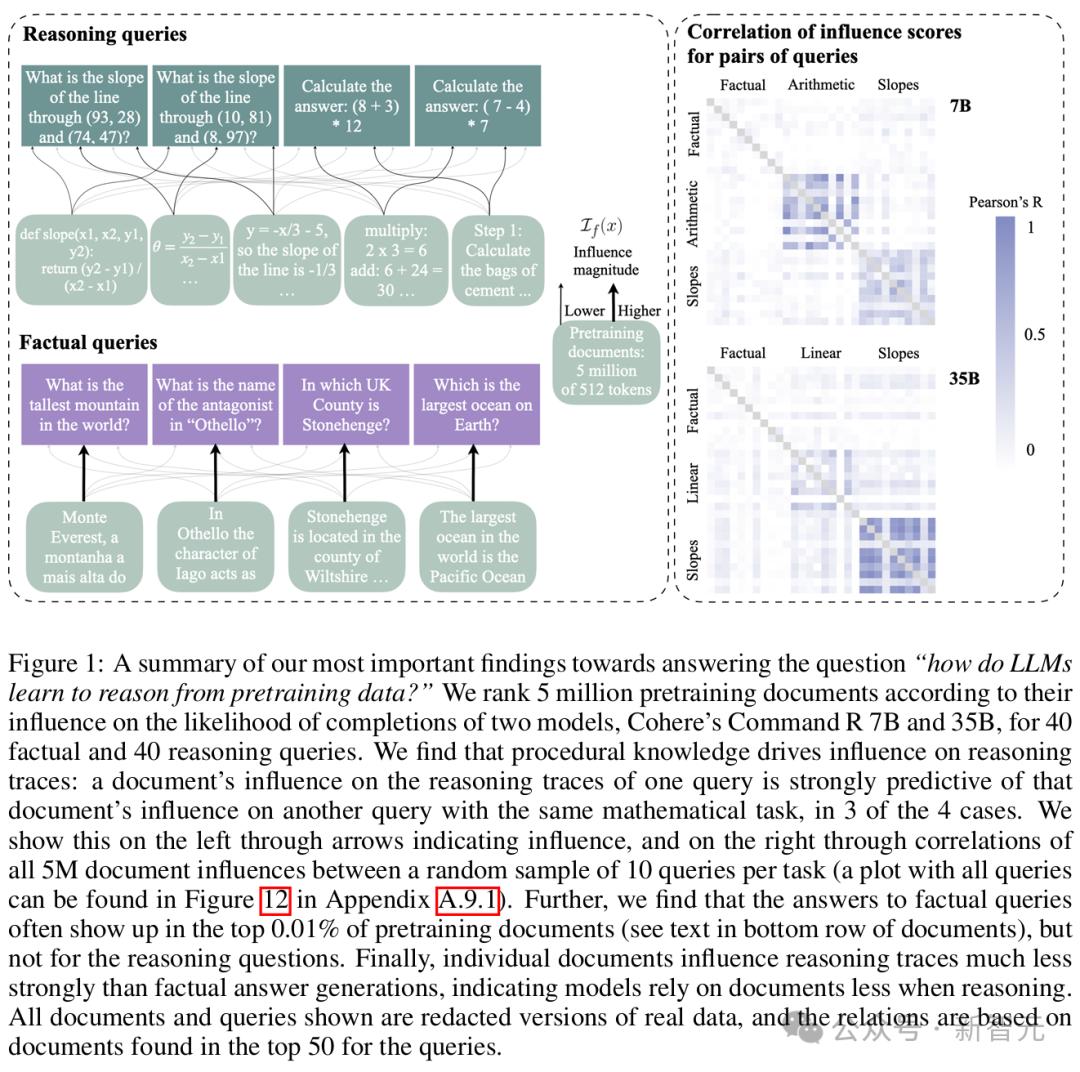
1. 文檔中的程序性知識,驅動了對推理過程軌跡的影響
一個文檔對某個查詢推理過程軌跡的影響力,可以強烈預測該文檔對相同數學任務的另一個查詢的影響力。
相比之下,這種現像在事實性查詢中卻並不成立。
這表明,對於需要將相同程序應用於不同數字的問題,文檔通常具有類似的貢獻。
在斜率計算的查詢中,這種相關性尤其顯著。在排名前0.002%的預訓練數據中,多次發現了包含代碼或數學解題程序的文檔。
2. 在推理問題上,模型對單個文檔的依賴程度較低,且依賴的文檔集合更為廣泛
研究人員還發現,對於模型生成的每單位查詢信息,文檔的影響力在推理問題上通常比事實性問題低得多。
此外,文檔集合的整體影響力波動性較小。
前者可以表明,在生成推理過程軌跡時,模型對每個單獨文檔的依賴程度低於事實性檢索。
而後者表明,對於一個隨機的25億預訓練token子集,是否包含高度影響力的文檔對事實性問題的影響更具偶然性,而對推理問題則更為穩定。
總之,這就表明,模型在推理問題上更傾向於從更廣泛的文檔集合中泛化,而對單個文檔的依賴較少。
3. 對於事實性問題,答案通常出現在高度影響力的文檔中,而推理問題則不然
查看每個查詢中排名前500(排名前0.01%)的影響力文檔後,研究人員發現,事實性問題的答案相對較常出現(7B 模型中佔55%的查詢,35B模型中佔30%)。
而在推理問題中,則幾乎沒有,即使他們確實在更大的25億token數據集中找到了答案。
4. 代碼對於數學推理非常重要
在推理查詢的正負影響力排名的頂端部分,與訓練分佈相比,代碼數據的比例明顯過高。
這個研究結果表明,推理的泛化策略,不同於從預訓練期間形成的參數化知識中進行檢索。
相反,模型的學習,是從涉及類似推理過程的文檔中提取程序性知識,無論是以程序的一般描述形式,還是以類似程序的應用形式。
這個發現告訴我們:或許我們並不需要在預訓練數據中涵蓋所有可能的情況。
相反,專注於展示跨多樣推理任務的程序性高質量數據可能更為有效,因為這有助於降低預訓練數據的冗餘性。
而代碼在所有任務中發揮的重要作用,也引發了一個有趣的問題:是否存在某種預訓練數據類型(例如代碼),能幫助模型(尤其是更大的模型),來學習多個任務?
如果能深入理解程序性泛化的範圍,我們未來的預訓練策略就會得到更多的指導,還能在數據選擇中確定重點。
文檔對補全的影響
影響函數
給定一個預訓練模型θ^u,該模型參數化了一個基於提示詞
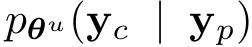
的下一個token的分佈。
其中,y_c = {y_1, …, y_m} 是補全,y_p = {y_1, …, y_n} 是提示詞,u表示參數未必訓練到收斂,研究人員希望找到來自預訓練數據集
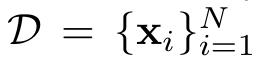
中對補全產生影響的數據。
也就是說,研究人員想知道,預訓練數據集中哪些樣本「導致」了一個補全。
為此,他們使用了針對大規模Transformer的EK-FAC影響函數。
參數 θ^u通常通過對目標函數執行基於梯度的迭代算法,並根據某些標準停止來獲得。
研究人員希望瞭解訓練文檔x_j∈D對參數θ^u的影響(通過鏈式法則,也可重新表述為「對θ^u的任何連續可微函數的影響」)。
研究人員希望,可以通過從原始訓練集中移除x_j,重新訓練模型,並將結果參數集(或其函數)與原始訓練模型進行比較,從而精確計算影響。
然而,對於任何有意義數量的文檔和參數來說,這種方法都是不可行的。
為此,他們利用影響函數通過對響應函數進行泰萊展開,來估計這種反事實:
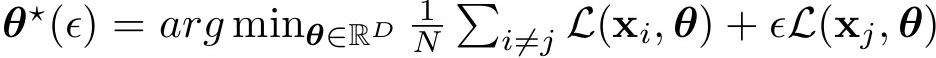
其中 L(·) 是一個損失函數,例如交叉熵損失。
響應函數在ε=0附近的一階泰萊近似,用於推導當ε改變時最優參數如何變化,而ε的變化會改變想要分析的文檔的權重。
通過隱函數定理,影響定義為:
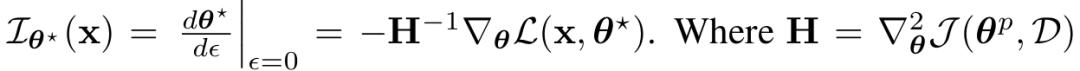
其中
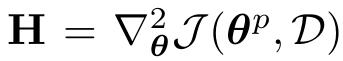
是預訓練目標的Hessian矩陣。
通過鏈式法則,可以通過近似以下公式,來估計給定提示詞時訓練文檔x = {x1, …, xk} 對補全的影響:
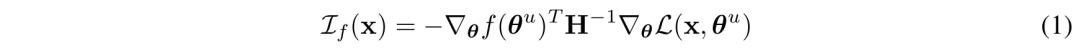
由於研究的是數十億參數D的模型,上述Hessian是不可計算的,因此,研究人員使用EK-FAC估計法來進行估算。
它涉及估算兩個期望值
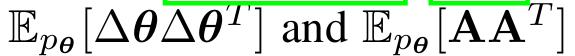
,其中A表示模型的激活。
為了使這種估算可行,研究人員在所有估算中做出了一些簡化假設,例如假設層與層之間相互獨立,並且只考慮 Transformer層的MLP參數。
 近似假設列表
近似假設列表應用EK-FAC
先前的研究表明,與其他類型的影響函數相比,EK-FAC影響函數能夠更準確地估算由響應函數給出的反事實。
然而,除了對語言模型補全的影響,研究人員還關注對訓練語言模型在回答問題時準確性的影響。
因為目前尚無研究表明,影響函數可以估算由下一詞預測生成文本的底層準確性的影響,因此只能計算對連續可微函數的影響。
因此,研究人員選擇交叉熵損失函數(公式1中的f)作為連續可微函數。
通過這種方式計算出的影響,可以揭示對7B模型在推理和閱讀理解任務中準確性具有因果影響的文檔。
具體來說,如果根據文檔的影響從微調數據中移除文檔並重新訓練模型,其準確性下降的幅度顯著高於隨機移除相同數量的文檔,或者使用梯度相似性移除相同數量的文檔。
同時,可以通過展示EK-FAC對Hessian的估算顯著優於僅使用一階信息的方法,來論證使用EK-FAC估算的合理性。
由於只能對預訓練數據樣本進行一次循環,並且只能在內存中存儲一個查詢梯度(其內存複雜度與模型本身相同),研究人員使用了奇異值分解(SVD)。
由於他們採用了一種基於概率算法的近似SVD,這顯著加快了查詢梯度的計算速度。
通過近似公式1來為預訓練數據D中的文檔計算得分,這些得分代表了它們在給定提示詞y_p時對補全y_c的影響。
在由響應函數近似的反事實問題中,影響得分為1,表示序列y_c的對數概率增加了1。
為了比較不同補全(和token長度)的影響得分,研究人員通過補全y_c的信息量對查詢得分進行歸一化,信息量以nat為單位衡量。
根據影響得分,他們對文檔進行了從正到負的排名,其中得分可以解釋為每nat查詢信息增加(或減少)的對數概率。
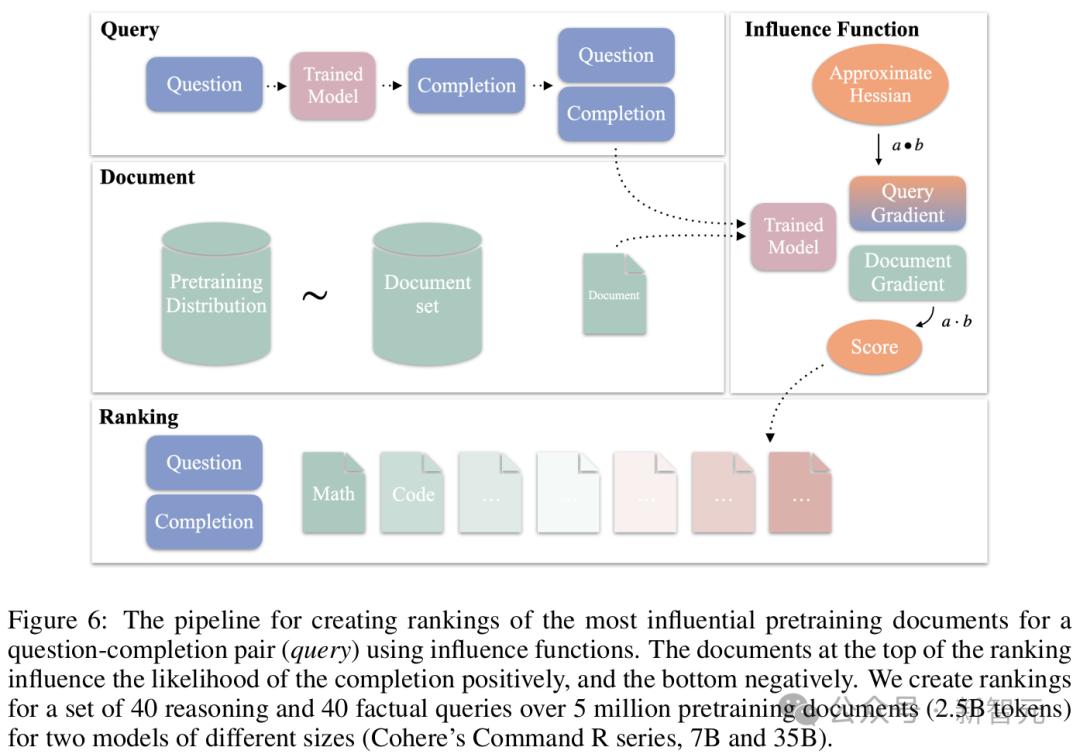
實驗與結果
實驗階段,研究人員比較了通過影響函數對推理問題生成的預訓練數據排名順序(從最正面影響到最負面影響)與事實性問題排名順序的差異(事實性問題只能通過檢索參數化知識來回答)。
定量分析
發現 1:對於底層推理任務相同的查詢,其文檔影響評分之間存在顯著的正相關性。這表明,這些文檔對需要相同程序但應用於不同數字的問題具有相關性。
如果模型依賴於包含「通用」知識的文檔,而這些知識適用於同一任務的所有查詢,那麼可以預期,這些查詢對應的文檔影響評分之間會呈現顯著的相關性。
研究人員通過計算所有500萬個文檔在所有查詢組合中的Pearson相關係數發現,對於相同類型推理任務的許多查詢之間,文檔評分存在顯著的正相關性;而對於大多數事實性查詢或不同類型推理查詢的組合,這種相關性則顯著缺失。這一現象表明,許多文檔對同類型推理問題具有類似的影響。
考慮到每種類型的推理查詢都需要將相同的程序應用於不同的數字,正相關性進一步說明,推理查詢的文檔影響評分能夠捕捉到程序性知識。
隨後,研究人員通過使用一組對照查詢(看起來相似,但不需要任何推理)並重覆整個實驗,否定了「推理問題之間的相關性僅由表面相似性導致」的假設(大多未觀察到相關性)。
此外,研究人員還通過不同查詢集之間高相關性或低相關性的具體示例,進一步驗證了程序性知識的作用——部分相關性由推理步驟的格式決定,而大部分則由推理程序本身決定。

發現 2:與回答事實性問題相比,模型在進行推理任務時,平均每生成一個單位信息(nat)所依賴的單個文檔程度較低,同時總影響的波動性也更小。這表明模型傾向於從更廣泛且更通用的一組文檔中進行泛化。這一現像在更大的模型中表現得尤為明顯。
具體來說,研究人員從兩個模型中觀察到以下兩點:
1. 首先,對於大多數事實性問題,在排名的任何部分,總影響均高於推理問題。這表明,事實性問題對文檔的依賴更為集中。
2. 其次,在不同的事實性查詢中,相同排名位置的文檔影響力變化更大。而對於少數事實性查詢,其總影響實際上低於推理查詢。
第一個結果表明,平均而言,模型在生成推理過程軌跡時,對單個文檔的依賴程度低於回答事實性問題。
第二個結果表明,對於事實性問題,模型更依賴於「特定的」且不常見的文檔。換言之,對於一個事實性問題,預訓練樣本中是否包含相對高影響力的文檔更依賴於偶然性
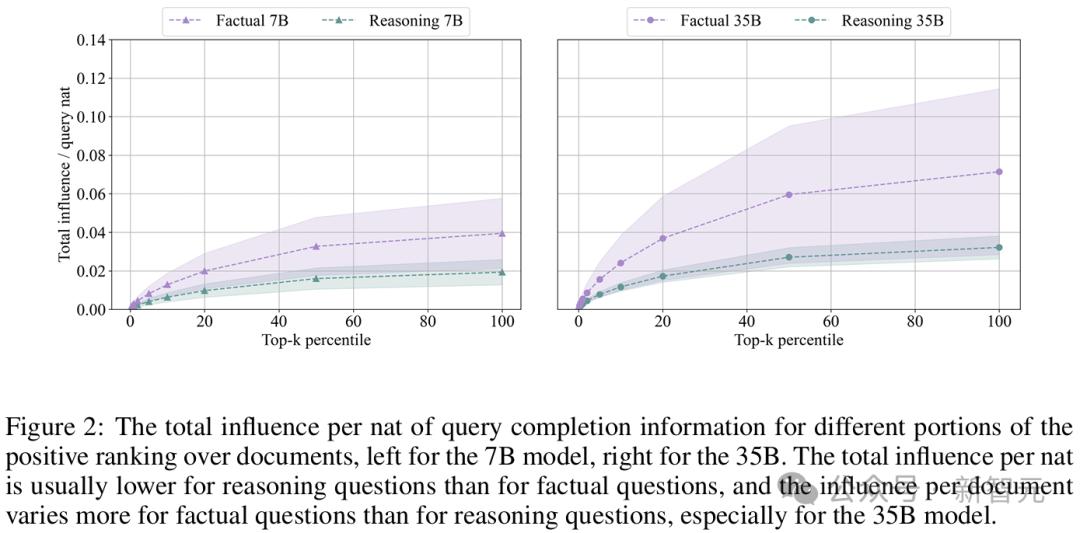
分析影響大小的另一種方法是觀察排名中影響的分佈。
結果顯示,文檔排名的頂部遵循冪律分佈,其特徵是在對數-對數空間中,排名與每單位信息增量(nat)的影響之間呈線性關係。
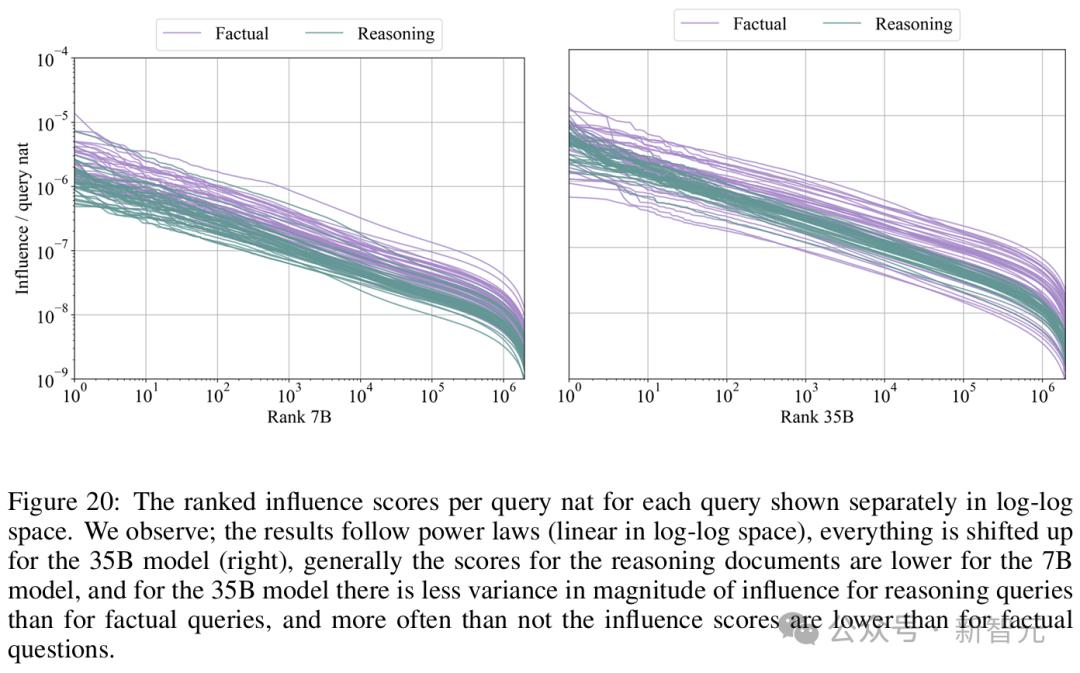
其中,對於35B模型的推理問題,其斜率比事實性問題略陡。
這意味著,在35B模型的推理問題中,排名頂部所包含的正面影響百分比,增長得比事實性問題更快。也就是說,推理問題的影響更集中於排名前列。
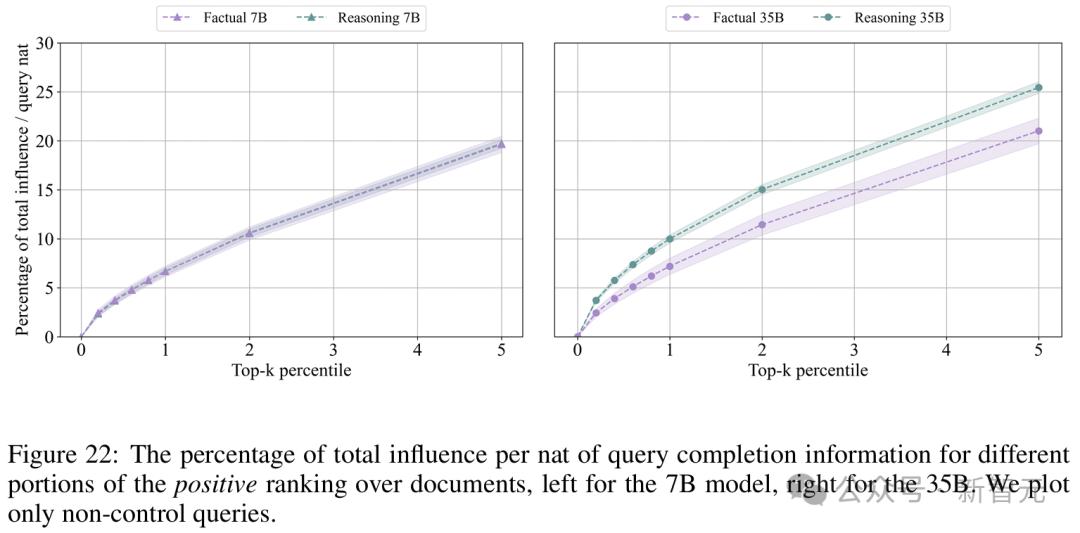
對於7B模型,模型正確回答推理問題的斜率平均也比事實性問題略陡,但當比較所有事實性問題和推理問題的斜率時,這種效果消失了。
這表明,對於35B模型,排名頂部序列所覆蓋的總正面影響百分比在推理問題中高於事實性問題。
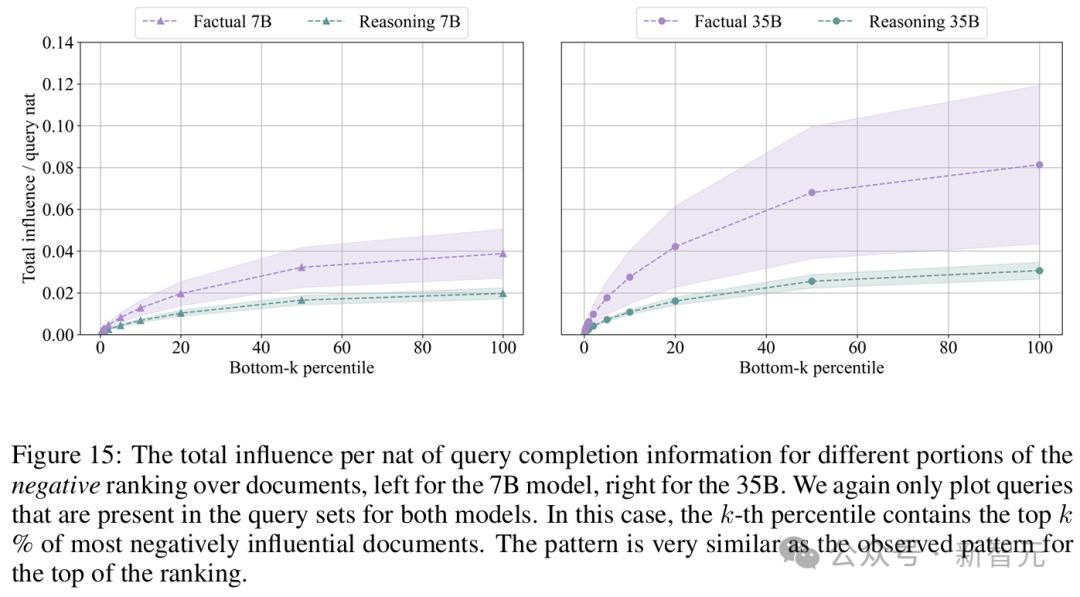
如果比較模型之間的結果,35B模型在整個排名中的影響和波動性差異更為顯著。
即使僅對兩個模型相同的查詢進行比較,這種效果依然存在,這表明較大模型的數據效率更高。
定性分析
除了定量分析之外,研究人員還對每個查詢的排名頂部進行了三項定性分析:
首先,搜索答案;
其次,分析文檔與推理查詢之間的關係;
最後,調查這些文檔來源於哪些數據集。
為了過濾掉一些無關信息,研究人員將影響分數除以文檔梯度範數並重新排序。
發現 3:對於事實性問題,答案相對較頻繁地出現在最具影響力的文檔中,而對於推理問題,幾乎不會出現。
為了在排名靠前的文檔中手動找到查詢問題的答案,研究人員為每個查詢構建了一組關鍵詞。如果答案存在於文檔中,這些關鍵詞應當出現在文檔中。
例如,對於事實性查詢,關鍵詞包括「tallest」、「highest」、「Mount Everest」(珠穆朗瑪峰)、「29029」和「8848」。而對於推理查詢,則為每個查詢構建了更多的關鍵詞,如「7−4」、「3」、「21」、「3∗7」,以及將操作替換為諸如「minus」(減)和「times」(乘)等單詞。


此外,研究人員為Command R+模型設計了一套提示詞,用於在查詢-文檔對中尋找答案,並利用它在每個查詢的前500個文檔中搜索答案,而不依賴關鍵詞重疊。
然後,手動檢查這些命中,並記錄包含查詢答案的文檔。(Command R+不僅找到了所有手動識別出的答案,並且還發現了更多答案。)

最後,將關鍵詞重疊搜索與Command R+提示詞相結合,應用於2.5B預訓練token的子集,以驗證答案是否存在於整個數據集中,而不只是前500個文檔。
結果顯示,對於7B模型,可以在前500個文檔中找到55%的事實性查詢的答案,而推理查詢僅有7.4%找到了答案。
對於35B模型,事實性查詢的答案在最具影響力的文檔中出現的概率為30%,而推理集合中則完全沒有答案。
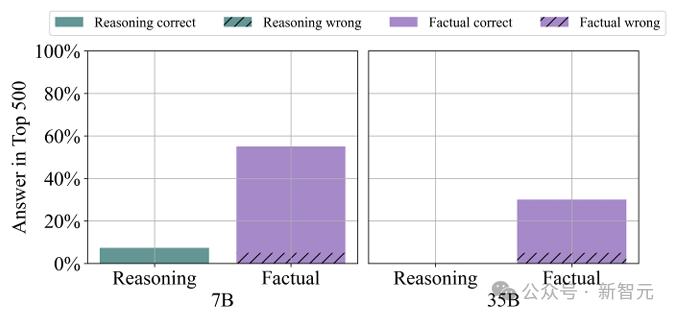

有趣的是,事實性問題的答案經常以不同的語言出現,例如西班牙語或葡萄牙語。
為了證偽「推理問題的答案未出現是因為它們不存在於500萬個文檔集合中」這一假設,研究人員在500萬文檔的隨機子集中重覆了上述關鍵詞搜索。
在20個算術查詢中,在未出現在前500個文檔中的文檔中識別出了13個推理步驟的答案,以及1個完整答案,並預計還存在更多未被關鍵詞搜索捕捉到的答案。對於斜率和線性方程查詢,找到了3個未出現在前0.01%文檔中的推理步驟答案。

發現 4:對於推理查詢,具有影響力的文檔通常也在進行類似的逐步推理,例如算術推理。此外,這些文檔通常通過代碼或數學方法實現了推理問題的解決方案。
對於斜率查詢,許多高影響力文檔展示了如何通過代碼或數學計算兩點之間的斜率。
對於7B模型,在20個查詢中的16個查詢中出現在前100個文檔中(共出現38次);而對於35B模型,這類文檔在所有查詢中都出現了(共出現51次)。
此外,研究人員還手動找到了7個通過代碼實現斜率計算的文檔,以及13個展示斜率計算公式的文檔。7B模型依賴於其中的18個文檔,而35B模型依賴於其中的8個。
以下是一個通過JavaScript(左)和數學公式(右)實現解決方案的高影響力文檔的示例:

隨後,研究人員提示Command R+對每個查詢的前500個文檔進行更詳細的特徵化分析。
結果顯示,這些文檔中通常涉及對其他數字進行類似的算術操作(如更大或更小的數字)、對相似數字進行類似的算術操作(如斜率問題),或對相似數字進行類似的代數操作(如求解線性方程)。
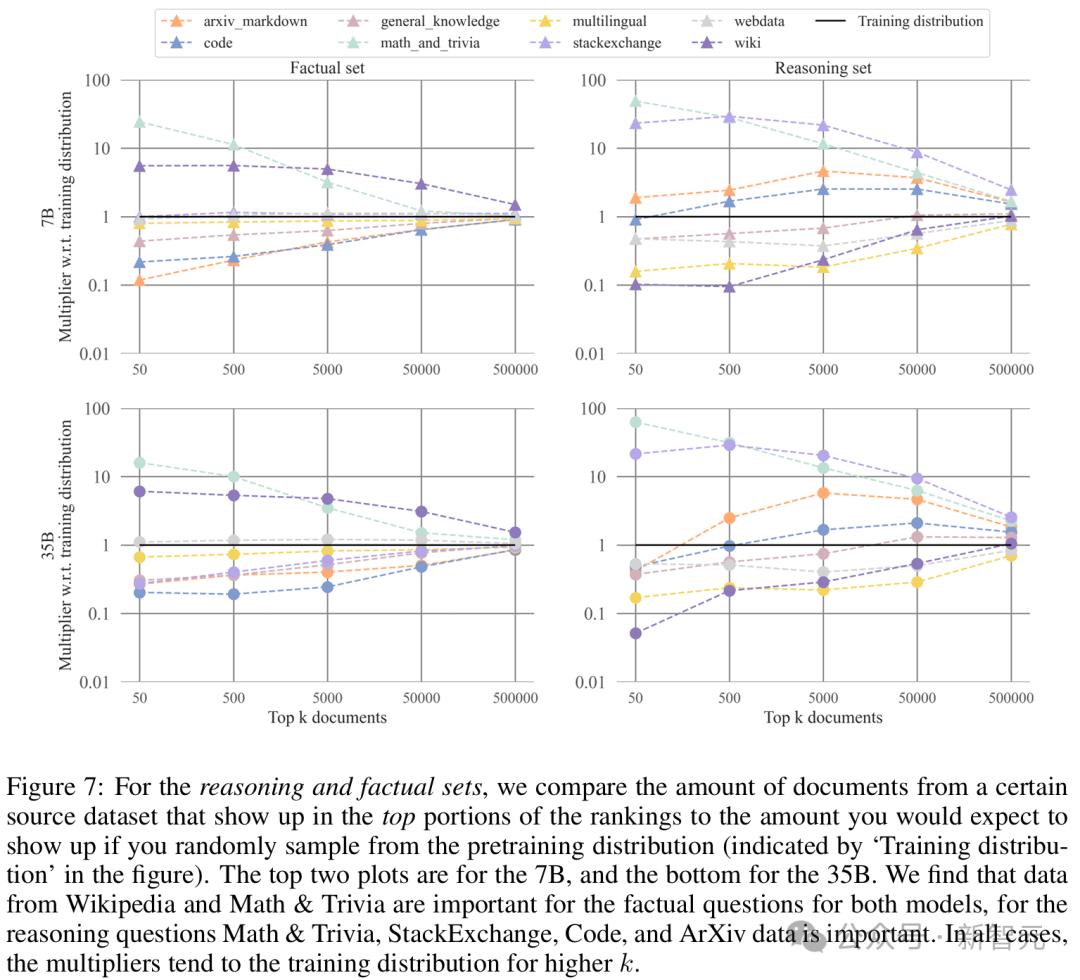
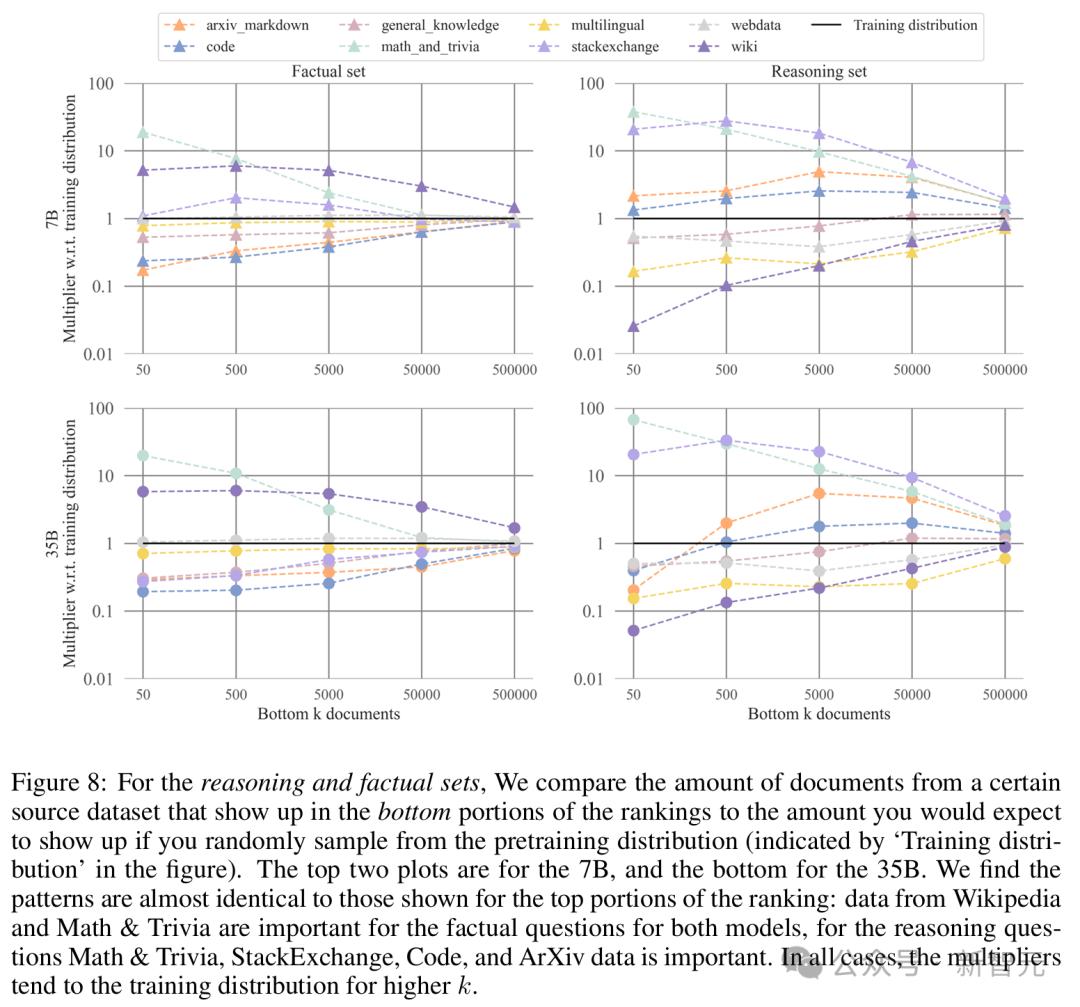
發現 5:對於事實性查詢,最具影響力的數據來源包括Wikipedia和trivia,而對於推理查詢,主要來源包括數學、StackExchange、arXiv和代碼。
研究人員分析了代表最具影響力文檔的源數據集的類型,並將該計數與預訓練分佈進行了比較。
作為數據來源的StackExchange,在排名頂部的數據中,其影響力是從預訓練分佈中隨機采樣時的十倍。其他代碼來源在從k=50到k=50000的範圍內,其影響力是隨機采樣時的兩倍。類似的模式也適用於排名底部的數據。
局限性
研究者也承認,方法存在重要的局限性。
最顯著的一點就是,沒有計算整個訓練集的影響,因為這在計算上是不可行的。
因此,研究結果可能存在另一種解釋,會讓人得出相反的結論:模型在推理時依賴的數據如此稀疏,以至於在隨機抽取的25億token中,任何一個推理查詢都未能浮現出相對高影響力的樣本。
這是否意味著,LLM在推理時會依賴稀疏和罕見的文檔呢?
也就是說,他們實際上是在研究一組對推理相對無影響的文檔,而如果觀察整個預訓練數據,推理路徑的答案可能會非常具有影響力。
然而,研究者認為這種解釋不太可能,原因有三。
第一,定性分析表明,推理問題的高影響數據直觀上高度相關,並且許多推理路徑的答案是25億token的一部分,只是對推理的影響力不高;第二,不同推理任務的影響分數之間的相關性顯著;第三,可以確認這些結果不適用於表面上與推理查詢相似但不需要逐步推理的對照查詢。
此外,模型從如此稀少的數據中,學習一種最簡單形式的數學推理(即對小數字的減法和乘法),可能性也極小。
另一個局限,就是沒有研究監督微調階段。
綜上所述,可以認為,結果表明了一種依賴程序性知識的泛化策略。
儘管如此,對於這類可解釋性研究的本質是,他們也只能提供證據,而非證明。
參考資料:
https://arxiv.org/abs/2411.12580
本文來自微信公眾號「新智元」,作者:新智元,編輯:Aeneas 好睏,36氪經授權發佈。