OpenAI o1是真有實力，港大權威AB測試，國家隊奧數題照樣拿下

OpenAI o1的數學推理能力是否真的那麼強？近日，來自港大的研究人員對模型進行了嚴格的AB測試，在非公開的國家隊奧數題面前，o1證明了自己的實力。

國際奧數題手到擒來，OpenAI o1是靠死記硬背還是真的實力超群？

近日，來自港大的研究人員對o1進行了嚴格的AB測試：

如何判斷LLM是否真正具有強大的數學推理能力？

考兩張卷子：一張是有可能提前背題的，另一張是不太可能提前背題的，兩張卷子難度一致。

如果LLM兩次考試的分數差不多，就證明人家是真會；要是後者的成績明顯低於前者，那就有作弊嫌疑了。

本文中，OpenAI Orion-1模型面對的兩張試卷，分別取自國際數學奧林匹克（IMO）和中國國家隊訓練營（CNT）的試題。

IMO的題目很容易獲得，而CNT的題目則無法公開訪問，通過比較o1模型在兩個數據集之間的性能，作者得出結論：o1是真有實力！

論文細節

OpenAI o1的亮相直接掀起了推理模型的風潮。 

o1採用強化學習來訓練token-wise獎勵模型，模擬了推理和反思過程，從而在token生成中培養了一種內在的思維鏈風格。

從本質上講，o1的推理是一個製定和執行計劃的過程。

OpenAI曾表示，o1-mini在美國高中AIME數學競賽中的分數可以排進全美前500，但也有一些評測表示o1的效果並不理想。

上奧數題

為了公平測試o1的數學推理能力，本文的研究者編譯了兩個數據集進行分析。

第一個數據集包含來自過去十年國際數學奧林匹克競賽（IMO）的60個問題；第二個數據集包含來自中國國家隊（CNT）訓練營的60個問題（非公開）。

註：CNT訓練營旨在為學生在中國的IMO比賽做好準備。中國國家隊的選拔過程涉及多次測試（通常為8-10次），每次持續4個半小時，與實際IMO比賽的形式相同。

針對測試事先作出假設：

原假設：o1-mini的問題解決能力是基於推理能力的；

備擇假設：o1-mini的性能可能來源於對問題和解決方案的記憶，或對預訓練模式的模仿。

對於原假設，可以預計模型在IMO和CNT數據集中表現出類似的性能水平。相反，在備擇假設下，o1在兩個數據集之間將存在顯著的性能差異（IMO數據集的得分更高）。 

另外，原假設還表明o1-mini能夠將其推理技能推廣到不同的問題集中，而不管它們的來源或複雜性如何。

實驗測試

latex是編寫數學問題和編輯軟件的標準格式，這裏將三個數據集從PDF轉換為latex文件，以便o1可以輕鬆讀取和處理。

o1不需要CoT這種額外的提示，實驗中直接將latex問題文件提供給 o1-mini模型。

評測採用IMO或CNT數學競賽中採用的標準評分方法：每道題最多7分；當問題需要數字答案時，提供正確的數字將獲得1分；如果解決問題的直觀方法是正確的，則獲得2分；其餘4分保留用於展示細緻準確的推理步驟。

在嚴格數學領域，推理的複雜性和邏輯步驟的精確性非常重要，而LLM所擅長的整體概念理解在評分過程中受到的重視相對較低。

對於以證明為導向的問題，評分系統將2分分配給基本正確的思維鏈（表明解決方案的邏輯路徑）；其餘5分取決於LLM能否給出詳細而嚴格的論點，強調數學證明中連貫推理的必要性。

修改標準

在評估o1-mini的響應時，作者觀察到模型難以始終如一地提供嚴格的證明步驟。

與正式證明相比，o1-mini通常表現出「試錯法」：進行了一系列嘗試，偶爾通過非正式推理和啟髮式猜測得出正確答案，這種非正式的推理缺乏數學證明所期望的嚴謹性和正式性。

下圖展示了一個例子，o1-mini通過驗證一些只涉及小自然數的情況來「猜測」答案。

基於o1-mini的這種特性，下面就不再要求正式的證明，而側重於評估模型展示正確直覺並通過推理得出正確結果的能力。

新的評價標準根據性質將問題分為兩種不同的類型：

1. 搜索類型：這類問題需要找到特定類型的數字、整數或基於表達式的解決方案，比如下面這個例子：

2. 解決類型：這類問題涉及尋找方程或優化問題的解決方案。

評分過程由精通相關數學領域的人工評估員負責。所有問題集、等級和相應的標籤都可應要求進行審查，從而確保評估結果的透明度和可訪問性。

結果評估

下表展示了兩個數據集（IMO和CNT）上不同類型問題的分佈情況。

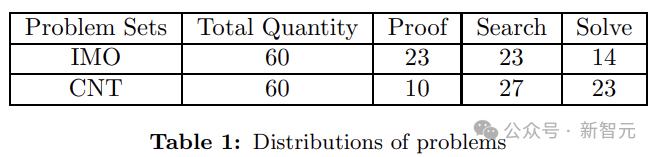
實驗的關鍵評估指標是，檢查o1-mini能否在Search和Solve類型的問題中提供正確的答案，結果如表2中所示。

第一列展示了o1-mini在搜索類型問題上的實際準確率（包括23個IMO問題和27個CNT問題），最後一行統計量t的計算公式如下：

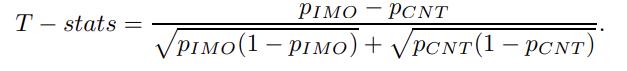
對於「Search」和「Solve」類型的問題，統計量t都非常接近0，這表明公共數據集（IMO）和私有數據集（CNT）之間，o1-mini模型的性能沒有統計學上的顯著差異。

也就是說，o1-mini的能力不是來自簡單地記住解決方案，而是源於其推理能力。

案例研究

o1通常以敘述風格編寫的思維過程和以數學嚴謹的語言編寫的最終解決方案。

在某些情況下，思考過程中提供的直覺可能是關鍵的一步。此外，在最終解決方案部分突出的邏輯錯誤也很普遍，例如在回答搜索類型的問題時未能論證其他解決方案不存在。

第一個例子題目如上圖所示，兩人輪流佔位，對Amy的額外要求是兩點之間的距離不能等於√5，求Amy最多能佔多少個位置。

首先，o1-mini分析了√5的限制（即兩點的坐標差為（1，2）或（2，1）），可以等效成下圖黑白點的站位，此時相同顏色的點距離都不會等於√5。

於是，O1-mini得出結論，Amy應該將她的石頭放在相同顏色的點上。

在這個例子中，o1-mini提供了有用的直覺，並給出了正確答案，但 模型也沒有解釋為什麼Amy不能佔更多的點。

對於上圖的問題，o1-mini測試了從1到18的整數，然後選擇了幾個較大的數字。通過分析滿足條件的數字，它發現了只有質數的冪才可行的模式。

然後，o1-mini正確地證明了為什麼質數的冪通常是可行的。然而，對於其他合數，o1-mini只提供了一些例子來說明。

在這個問題中，o1-mini堅持測試小的、易於計算的案例，這種方法在大多數搜索類型的問題中很常用，而且一般能拿到大部分分數。

下一個問題，找出所有符合條件的實數：

對此，人類的推理過程一般首先考慮α是整數的情況，然後分別評估奇數和偶數兩個子情況，可以使用求和公式寫出結果並進行推斷。

實驗中，o1-mini以類似的方式開始，幾乎完美地複製人工解的步驟。對比細節可以發現模型的推理存在疏忽，比如沒有考慮整數份量的奇偶校驗（奇偶性不會影響實際答案）。

最後一個例子的推理稍微複雜一些，o1-mini終於做錯了。它這次選擇了暴力破解：遍曆每一列，直到找到怪物或到達最後一行。

雖然o1-mini正確識別出有一個安全的列，但它沒有認識到探索怪物下方以到達最後一行的重要性。

這表明o1-mini缺乏強大的空間推理能力（即使是在二維空間中），並且與人類相比缺乏解決問題的策略。它無法解決問題可能是由於缺乏公式化的分步方法，或是用來確定最有效算法的規則。

參考資料： 

https://arxiv.org/abs/2411.06198 

本文來自微信公眾號「新智元」，作者：新智元，36氪經授權發佈。