圖學習新突破：一個統一框架連接空域和頻域

AIxiv專欄是機器之心發佈學術、技術內容的欄目。過去數年，機器之心AIxiv專欄接收報導了2000多篇內容，覆蓋全球各大高校與企業的頂級實驗室，有效促進了學術交流與傳播。如果您有優秀的工作想要分享，歡迎投稿或者聯繫報導。投稿郵箱：liyazhou@jiqizhixin.com；zhaoyunfeng@jiqizhixin.com

陳枳扡博士：現任密西西比州立大學計算機系助理教授，專注於圖機器學習及應用領域，在譜域視角與不確定性研究方面著力頗深。其研究成果見諸於 AAAI、IJCAI、ACM、ICDM、EMNLP、Computing Surveys、Nature Communication 等。他的科研工作承蒙美國國家科學基金會（NSF）及美國農業部（USDA）多個項目的資助，且榮獲豐田研究院傑出貢獻獎與 ACM SIGPSATIAL 2020 最佳論文獎。

張磊博士：於 2024 年畢業於維珍尼亞理工後，以助理教授身份加盟北伊利諾伊大學。他的研究興趣廣泛覆蓋機器學習和數據挖掘範疇，尤其聚焦於圖神經網絡、圖結構學習、雙層優化、神經架構搜索以及社交網絡挖掘等方面。在 AAAI、ICDM 等頂級會議上發表多篇論文，並於 2023 年夏季斬獲維珍尼亞理工大學的 Cunningham Fellowship。

趙亮博士：身為埃梅利大學計算機系副教授，他的研究領域橫跨數據挖掘、人工智能等多學科，在圖學習領域成果斐然。在 KDD、NeurIPS、AAAI、IJCAI、WWW 等眾多頂級會議及期刊上發表超百篇論文，屢獲殊榮，如 NSF CAREER 獎、Meta Research 獎、Amazon Research 獎等，還榮獲 ICDM 2022 最佳論文獎、ACM SIGPSATIAL 2022 最佳論文獎以及 WWW 2023 最佳論文提名等。

圖數據學習在過去幾年中取得了顯著的進展，圖神經網絡（GNN）在此過程中起到了核心作用。然而，不同的 GNN 方法在概念和實現上的差異，對理解和應用圖學習算法構成了挑戰。

針對這一問題，來自密西西比州立大學，北伊利諾伊大學和埃梅利大學的學者通過一系列教程對此問題展開了討論，這些教程展示在 CVPR 2024、CIKM 2024、SIAM Math and Data Science 2024，以及發表在 Computing Surveys 的一篇論文: 《Bridging the Gap between Spatial and Spectral Domains: A Unified Framework for Graph Neural Networks》。

論文地址：https://dl.acm.org/doi/10.1145/3627816

問題：統一框架的突破意義何在？

儘管圖神經網絡已經在多個領域展示出了卓越的性能，從化學分子識別到社交網絡分析，從交通網絡到輸電網絡，再到大腦網絡。GNN 也在不同的場景下，用不同的理論和機制來設計新的圖神經網絡，例如 Heat diffusion, page rank, random walk, attention model, ARMA, low-pass filtering。雖然展現了 GNN 和很多不同理論工具的連接性，但這也加劇了 GNN 領域的分裂。這些方法因為急於不同理論，無法進行理論上直接的比較。

Part 1: 圖學習理論框架的現狀

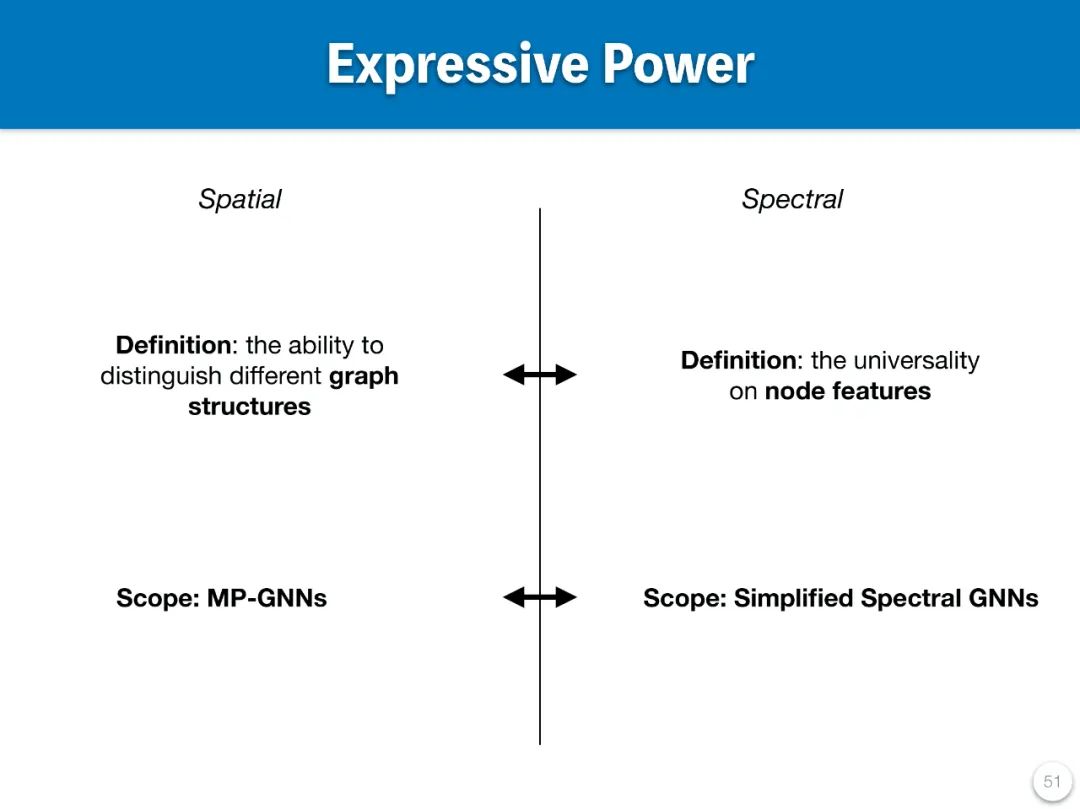
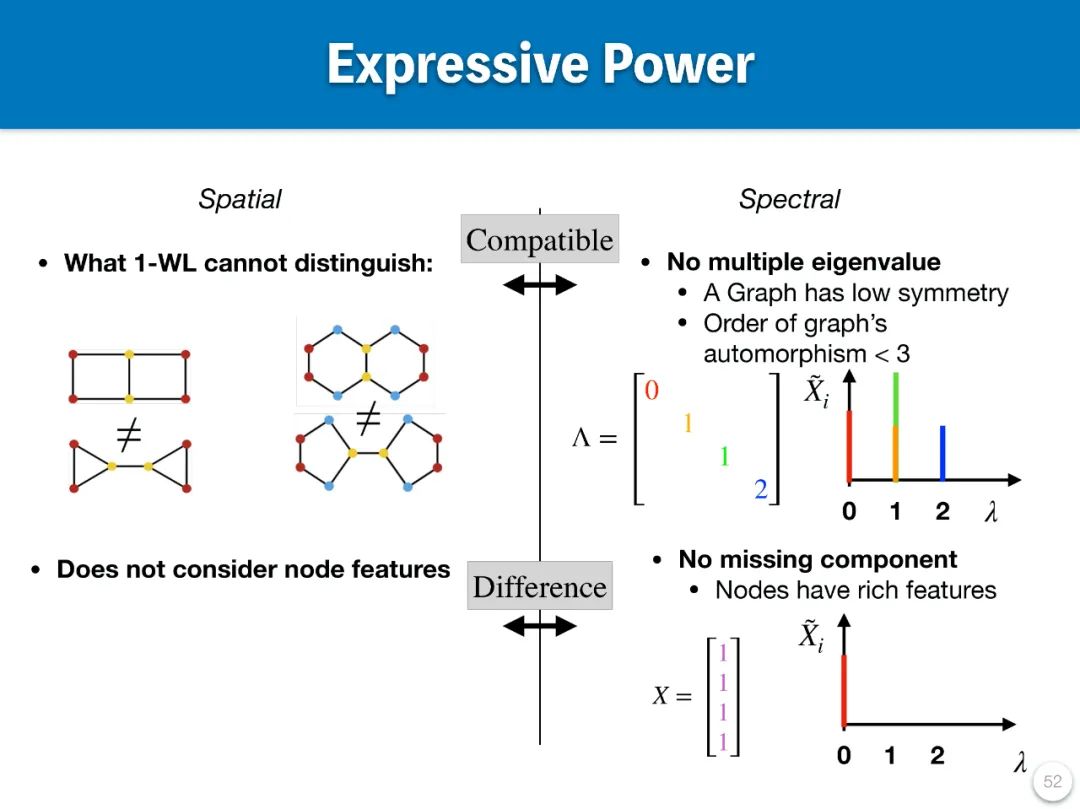
目前，圖神經網絡（GNN）涵蓋了多種模型和層的類型，但總體可以分為空域（spatial）圖模型和頻域（spectral）圖模型。針對這些模型，不少研究者嘗試提出通用框架，以便在同一框架下對不同模型進行分析和比較。然而，這些框架主要集中於空域圖模型。值得注意的是，有一類研究從統一的出發點 —— 即模型的表達能力（Expressive Power）—— 對空域和頻域圖模型進行了分析。儘管如此，空域和頻域圖模型在表達能力的定義上存在差異，其分析結論和設計建議既有共通之處，也各有不同，同時兩者均存在一定的局限性。

Part 2: 圖卷積

圖卷積可以通過譜圖理論（Spectral Graph Theory）中的圖傅里葉變換（Graph Fourier Transform）和卷積定理（Convolution Theorem）來理解。

圖傅立葉變換：圖的結構通過圖拉普拉斯矩陣（Graph Laplacian）來表示。拉普拉斯矩陣 L 可以進行特徵值分解：

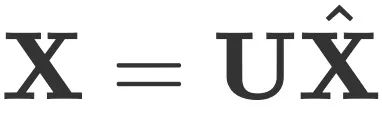
。通過這種變換，研究者可以在頻域中處理和分析圖信號。

。其逆變換為

轉換到頻域：

，其中 U 是特徵向量矩陣，∧ 是特徵值的對角矩陣。圖傅里葉變換就是將圖信號

卷積定理：在傳統信號處理中，時域的卷積等價於頻域的逐點相乘。對於圖信號，同樣成立：設兩個圖信號 X（輸入特徵）和 g（濾波器），它們的圖卷積定義為：

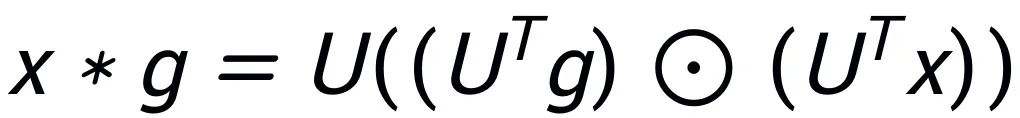
，它是特徵值 ∧ 的函數：

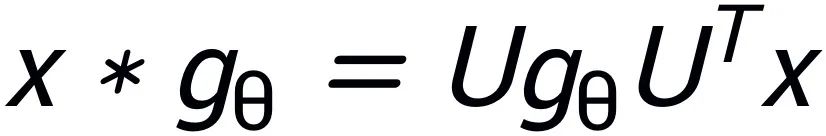
，其中 θ 是可訓練的參數向量。卷積操作可以寫為：

。其中，⊙ 表示頻域的逐點相乘，g 表示頻域濾波器。這表明圖卷積可以通過頻域操作實現。為了在圖神經網絡中實現卷積，濾波器 g 被參數化為

圖卷積網絡（GCN）在頻域和空域的解釋：在頻域圖模型中，GCN 使用的是

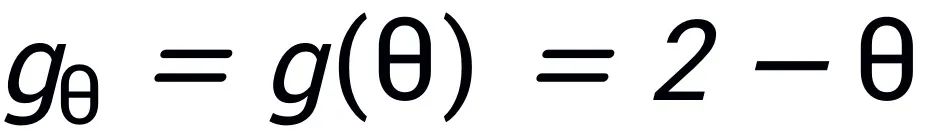
。這種操作本質上是一種固定的卷積操作，沒有可學習參數。由於歸一化之後的拉普拉斯矩陣的特徵值範圍為 0 到 2 之間，2-θ 的濾波器實際上是一個低通濾波器：放大低頻平滑信號，減弱高頻信號。在空域圖模型中， GCN 的操作可以理解為對每個節點的鄰居節點的特徵值進行求和，然後取平均值。這是一種基於鄰居特徵聚合的方式。GCN 的頻域和空域視角是等價的，但各有側重。頻域解釋更偏向理論上的信號處理本質，而空域解釋更貼近工程實現和直觀理解。對於研究者而言，這兩種視角是相輔相成的，結合使用可以更全面地理解和改進 GCN。

的一階近似，其中

Part 3: 新的統一框架：連接空域和頻域

教程中提出的框架基於一個核心假設：空間域和頻譜域的圖表示學習可以通過一個共同的數學語言進行描述。研究人員引入了一種新的圖嵌入方法，該方法結合了圖的空間連接性和節點特徵，能夠更加精準地捕捉和表示圖數據的複雜性。

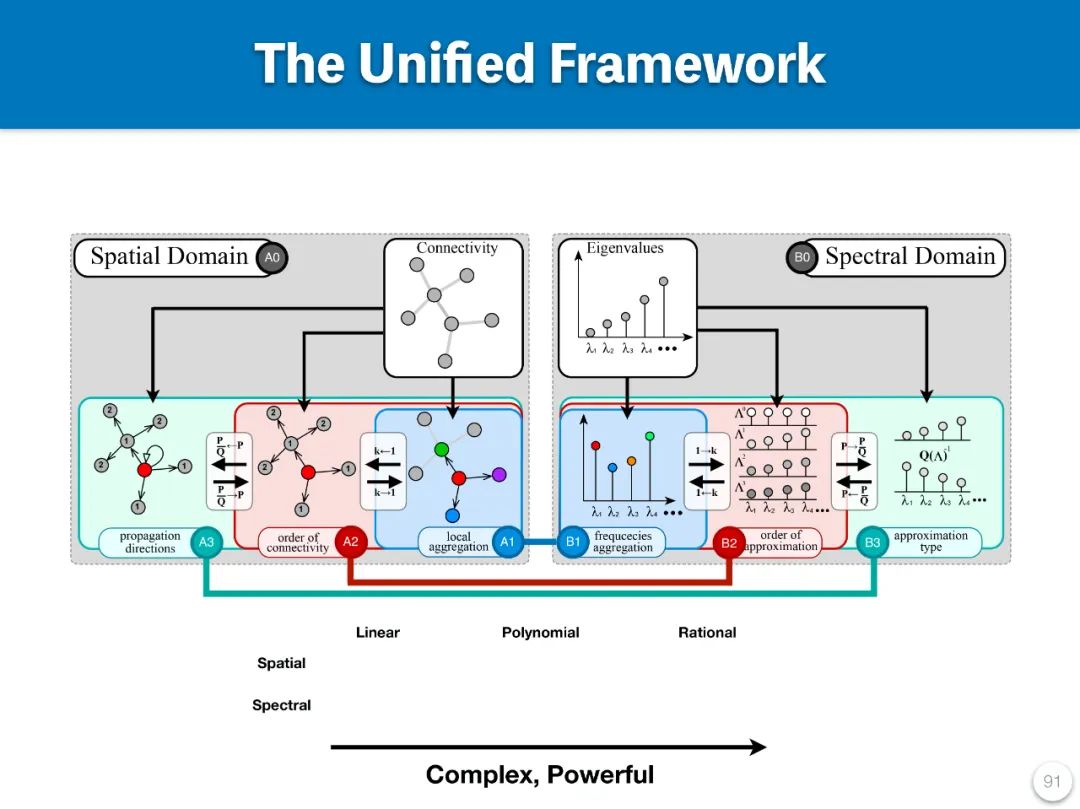
其他領域里頻域和空域的研究

在已存在的研究里，這種空域和頻域相互連接視角並不少見。研究者用兩個例子來說明：

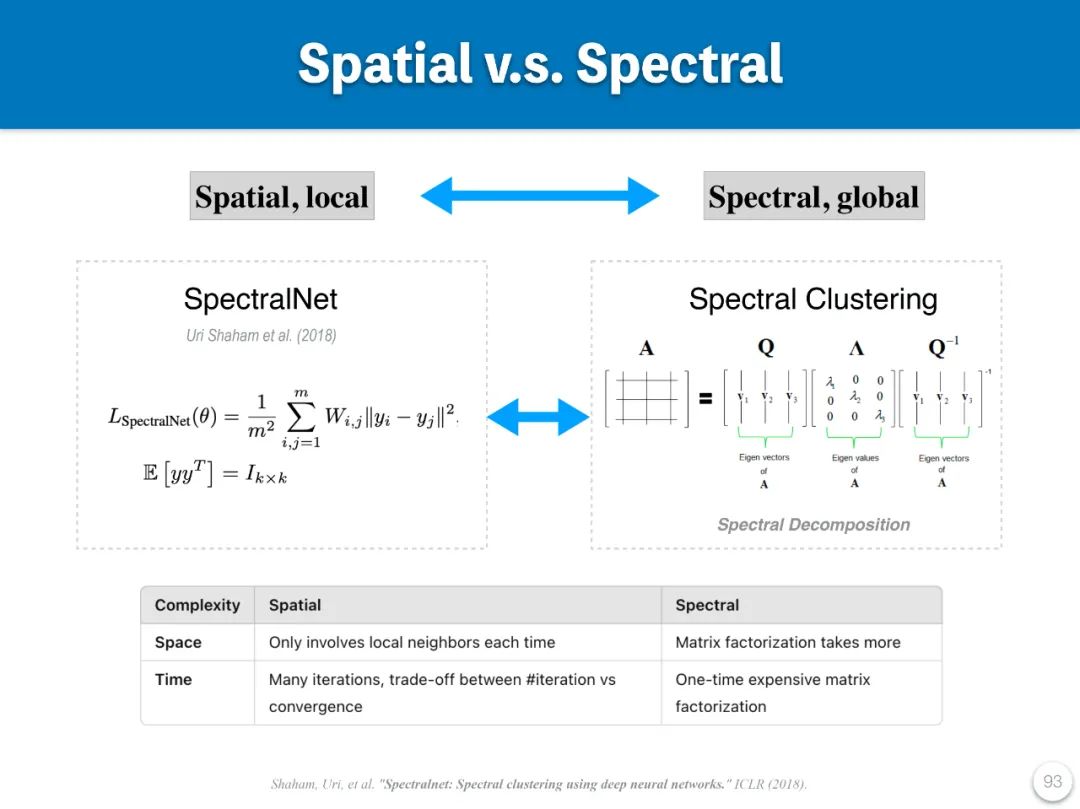
（1）譜聚類：從譜域的視角看譜聚類是使用譜分解 (spectral decomposition) 或則說特徵分解（eigen-decomposition），然後使用分解結果中特徵值響亮的低頻信號來作為新的表達，然後使用較為簡單快速的 Kmeans 得到聚類結果。而另外一個新的實現，SpectralNet，設計了一個特別 loss，使用神經網絡來得到幾乎一樣的結果。單神經網絡是一種以降低 loss 為導向的迭代算法，所以可以視為一種近似譜聚類的算法。

（2）另外一個例子是著名的 Word2Vec 算法。以 Skip-gram 為例，每個單詞都要相似於它的上下文的環境里其他單詞。所以 Word2Vec 是一個迭代算法。在後來的研究中，Levy 提出了一些分析，發現使用 Word2Vec 的結果里的矩陣，能夠幾乎完整的還原單詞的共現矩陣（PPMI）。也就是說 Word2Vec 可以看作是矩陣分解算法的一種近似算法。

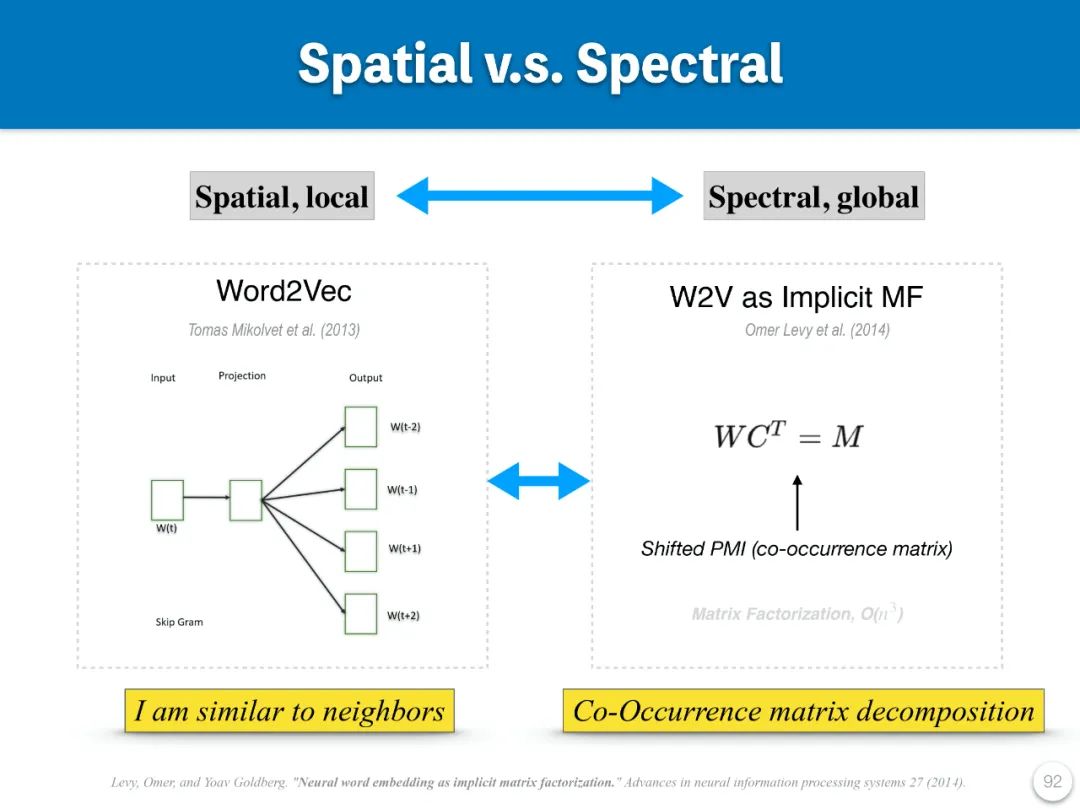
在這兩個例子中，研究者發現這種比較中，有類似於該研究提出的譜域和空域方法區別。即，一種方法側重矩陣分解，而另外一種側重於迭代近似。

Part 4: 未來方向展望

這項研究開闢了圖結構學習領域的新方向，未來的研究可以基於此框架進一步探索：

• 計算效率：如何進一步優化統一框架以處理大規模圖數據，在譜論表達下，圖的信息量依然巨大，對計算仍然是一個挑戰。

• 統一的譜論：目前譜論主要應用於靜態圖結構，而且是簡單圖（即無向，邊只連接兩個節點）。然後圖論中仍然有大量的不同類型的圖，缺少譜論的表達，例如有向圖，超圖，或則動態圖。

• 應用擴展：將統一框架應用到更多實際問題中，如生物信息學和社會網絡分析，如何解釋譜論視角下真實應用的規律，是一個值得探索的領域。