神經網絡為何非激活函數不可?
本文作者 Vandit Jain 對激活函數的相關知識進行了一個較為全面的總結,重點聚焦於以下幾個方面:
1. 激活函數是什麼,它在網絡中有什麼作用?
2. 為什麼需要激活函數而不使用線性函數?
3. 理想的激活函數有哪些特徵?
4. 目前使用的各種非線性函數。
5. 在最新研究中湧現的值得關注的非線性激活函數。
6. 在深層神經網絡中應該使用哪些激活函數以及如何使用它們?
一、激活函數是什麼?
簡單地說,激活函數就是加入到人工神經網絡中的一個函數,目的在於幫助神經網絡從數據中學習複雜模式。
相比於人類大腦中基於神經元的模型,激活函數是決定向下一個神經元傳遞何種信息的單元,這也正是激活函數在人工神經網絡中的作用。激活函數接收前一個單元輸出的信號,並將其轉換成某種可以被下一個單元接收的形式。
下圖總結了兩者的區別:
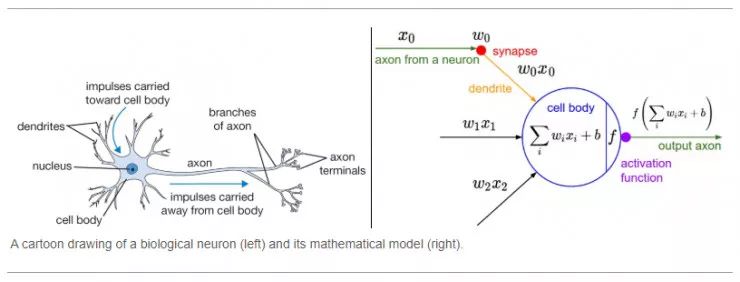 資料來源:史丹福大學的cs231n 課程
資料來源:史丹福大學的cs231n 課程二、為什麼需要激活函數?
在神經網絡中使用非線性激活函數的原因有很多。
1. 除了前面討論過的生物學方面的相似性外,激活函數還有助於我們根據要求將神經元的輸出值限定在一定的範圍內。這一點很重要,因為激活函數的輸入是 W*x+b,其中 W 是單元的權重,x 是輸入值,然後加上偏置 b。如果輸出值不被限定在某個範圍內,它可能會變得非常大,特別是在具有數百萬個參數的深層神經網絡中,從而導致計算量過大。例如,有一些激活函數(如 softmax)對於不同的輸入值(0 或 1)會輸出特定的值。
2. 激活函數最重要的特點是它具有在神經網絡中加入非線性的能力。為了便於理解,我們不妨考慮一下多維數據,如下圖所示:

線性函數有三個屬性(在這個圖中分別是體重,收縮壓和年齡),它使我們得到一條貫穿三維空間的直線,但它永遠也無法學會一種模式來將一個人準確地區分為吸煙者和不吸煙者(以手頭上現有的分類問題為例)。原因很簡單,定義這個分類的模式根本不是線性的。
那在人工神經網絡中,如果我們使用只有一個單元而沒有激活函數的神經網絡會怎樣?這種情況下我們所得到的輸出基本上還是 W*x+b,這並不好,因為 W*x 也是 x 的一次方,因此函數仍然是線性的,基本等同於線性函數。
如果我們疊加多層呢?假如我們用一個函數 f(x)來表示 nᵗʰ層,那麼可以得出:

然而,這還不夠複雜,特別是在計算機視覺或自然語言處理等有著複雜模式的問題中。
為了使模型能夠學習非線性模式(或者說具有更高的複雜度),特定的非線性層(激活函數)被加入其中。
三、理想的激活函數具有的特點
1. 梯度消失問題:神經網絡是利用梯度下降過程來訓練的。
梯度下降由基於鏈式規則的反向傳播組成,鏈式規則用於獲取權值變化以減少每次訓練後的損失。考慮一個兩層網絡,第一層表示為 f₁(x),第二層表示為 f₂(x)。整個網絡為 o(x)= f₂(f₁(x))。
如果我們反過來計算權重,可以得到 o`(x)= f₂(x)*f₁`(x)。這裏 f₁(x)本身是由 Act(W₁*x₁+b₁)組成的復合函數,其中 Act 是第 1 層之後的激活函數。再次應用鏈式規則,可以得到 f₁`(x)=Act(W₁*x₁+b₁)*x₁,這意味著此結果也直接依賴於激活值。現在可以看到, 這樣一個鏈式規則在反向傳播時會經過很多個層。
如果 Act()的值介於 0 和 1 之間,那麼它會乘以幾個這樣的值來計算初始層的梯度。這個過程會降低初始層的梯度值,並且這些層也無法正確學習。
換言之,因為網絡的深度和激活過程將值轉變為趨近於 0,它們的梯度逐漸消失,這就是所謂的梯度消失問題。所以我們希望理想的激活函數不要使梯度逐漸變為零。
2. 以零為中心:激活函數的輸出應對稱於零,這樣梯度就不會向特定方向移動。
3. 計算成本:網絡的每一層都會應用激活函數,它在深層網絡中需要計算數百萬次。因此,激活函數的計算成本應該很低。
4. 可微性:如前所述,神經網絡使用梯度下降過程進行訓練,因此模型中的層需要可微或至少部分可微。這是一個函數可以作為激活函數層的必要條件。
四、目前使用的各種非線性函數
1、Sigmoid 函數
函數如下圖所示:

這種激活函數從未在實際模型中使用,僅由於歷史原因羅列在此。Sigmoid 函數計算量大,會導致梯度消失問題且不以零為中心,通常在二進製分類問題中才會使用。
-
Softmax 邏輯回歸模型: softmax 邏輯回歸模型是 Sigmoid 函數在多分類問題上的一種推廣形式。與 Sigmoid 函數相似,它也產生 0-1 範圍內的值,因此被用作分類模型的最後一層。
2、雙曲正切函數 tanh
如圖所示:

相比於 Sigmoid 函數,它僅僅解決了以零為中心這個問題。
3、線性整流函數(Rectified Linear Unit, ReLU)
該函數又稱修正線性單元,定義為 f(x)=max(0,x):

這是一個使用十分廣泛的激活函數,尤其是在卷積神經網絡中。它計算簡單,不會飽和,不產生梯度消失問題,但不以零為中心。它也存在「dying ReLU」問題,即當輸入的是負數時,輸出都會變成零,這樣就導致一些節點完全「死掉」,神經元也不會進行學習。
ReLU 的另一個問題是激活爆炸,因為它的上限是 inf,有時會產生不可用的節點。
4、Leaky ReLU 和 Parametric ReLU 函數
函數的定義為 f(x)=max(αx,x),如下圖所示:

當α為0.1時
這裏α是一個通常設置為 0.01 的超參數。顯然,Leaky ReLU 在一定程度上解決了「dying ReLU」這一問題。請注意,如果我們將α設為 1,那麼 Leaky ReLU 將成為線性函數 f(x)=x,並且沒有任何用處。
因此,α的值永遠不會設置為趨近於 1 的值。如果我們分別將α設為每個神經元的超參數,則得到 Parametric ReLU 或 PReLU。
5、ReLU6 函數
ReLU6 在 x>0 的區域基本上等同於 ReLU,定義為 f(x)=min(max(0,x),6)

這有助於阻止激活增長,從而防止梯度爆炸(趨近無限時)以及正常 ReLUs 發生的其他小問題。
我們通常的想法是,為什麼不把 ReLU6 和 Leaky ReLU 結合起來,以解決現在的激活函數的所有已知的問題。流行的 DL 框架沒有提供現成的這樣的激活函數,但我認為這是一個很好的想法。
五、在最新研究中湧現的值得關注的非線性激活函數
1、Swish 函數
Swish 由 Ramachandran 等人在 2017 年提出,定義為 f(x)=x*sigmoid(x)。

與 ReLU 相比,儘管圖形非常相似,Swish 的性能卻要稍好一些。然而,ReLU 在 x=0 時會突然發生改變,而 Swish 與此不同,它不會在某個點上突然改變,這使得訓練時 Swish 更容易收斂。
但是,Swish 的缺點是它的計算成本很高,為瞭解決這個問題,我們來看看下一個版本的 Swish。
2、Hard-Swish 或 H-Swish函數
函數定義如下:

它最大的優點是幾乎類似於 swish 函數,但計算成本卻比 swish 更低,因為它用線性類型的 ReLU 函數取代了指數類型的 sigmoid 函數。
六、在深層神經網絡中如何使用這些激活函數?
首先,Tanh 和 sigmoid 函數會引起巨大的梯度消失問題,因此一般不推薦使用。
神經網絡中一開始嘗試引入 ReLU 函數。如上文所述,在權重層(諸如 CNN、RNN、LSTM 或線性感知層)之後添加激活層。如果你認為模型已經停止學習,那麼可以用 Leaky ReLU 替換它,以避免「Dying ReLU」問題。但 Leaky ReLU 會稍微增加計算時間。
如果網絡中也有 Batch-Norm 層(批標準化層),則需要在執行激活函數之前添加該層,順序是先進行 CNN-Batch(卷積神經網絡批處理),再進行 Norm-Act(標準化動作)。雖然 Batch-Norm(批標準化)和激活函數的運行順序是一個備受爭議的話題,也有人說順序其實無關緊要,為了與 Batch-Norm 的原論文保持一致,作者使用的是以上提到的這種順序。
激活函數的預設超參數如果是在如 Tensorflow 和 Pytorch等框架中使用,則效果最好。然而,你可以調整 Leaky ReLU 中的負斜率並將其設置為 0.02 以加快學習速度。