餘弦相似度可能沒用?對於某些線性模型,相似度甚至不唯一
機器之心報導
機器之心編輯部
好不容易找了把尺子,結果尺子會隨機伸縮。
在機器學習和數據科學領域,餘弦相似度長期以來一直是衡量高維對象之間語義相似度的首選指標。餘弦相似度已廣泛應用於從推薦系統到自然語言處理的各種應用中。它的流行源於人們相信它捕獲了嵌入向量之間的方向對齊,提供了比簡單點積更有意義的相似性度量。
然而,Netflix 和康奈爾大學的一項研究挑戰了我們對這種流行方法的理解:餘弦相似度可能導致任意且毫無意義的結果。

論文地址:https://arxiv.org/pdf/2403.05440v1
餘弦相似度通過測量兩個向量的夾角的餘弦值來度量它們之間的相似性,機器學習研究常常通過將餘弦相似性應用於學得的低維特徵嵌入來量化高維對象之間的語義相似性。但在實踐中,這可能比嵌入向量之間的非標準化點積效果更好,但有時也更糟糕。
圖源:https://www.shaped.ai/blog/cosine-similarity-not-the-silver-bullet-we-thought-it-was
為了深入瞭解這一經驗觀察,Netflix 和康奈爾大學的研究團隊研究了從正則化線性模型派生的嵌入,通過分析得出結論:對於某些線性模型來說,相似度甚至不是唯一的,而對於其他模型來說,它們是由正則化隱式控制的。
該研究討論了線性模型之外的情況:學習深度模型時採用不同正則化的組合,當對結果嵌入進行餘弦相似度計算時,會產生隱式和意想不到的效果,使結果變得不透明並且可能是任意的。基於這些見解,研究團隊得出結論:不要盲目使用餘弦相似度,並概述了替代方案。
最近,這篇論文在機器學習社區再度引起熱議,一篇題為《Cosine Similarity: Not the Silver Bullet We Thought It Was(餘弦相似度:不是我們想像的靈丹妙藥)》的博客概述了研究內容。

博客地址:https://www.shaped.ai/blog/cosine-similarity-not-the-silver-bullet-we-thought-it-was
有網民表示:「問題沒那麼嚴重,相似度指標需要根據嵌入空間進行量身定製,需要測試不同的指標來建立定性評估。」

網民認為餘弦相似度應該是一個足夠好的方法。畢竟,「根據 OpenAI 關於嵌入的文檔,他們還在代碼片段中使用了餘弦相似度。」

這個結論是怎麼得出來的呢?讓我們一起看看這篇論文的主要內容,一探究竟。
研究簡介
研究團隊發現了一個重要問題:在特定場景下,餘弦相似度會隨意產生結果,這使得該度量方法變得不可靠。
研究著重分析了線性矩陣模型。這類模型能夠得到封閉形式的解與理論分析,在推薦系統等應用中被廣泛用於學習離散實體的低維嵌入表示。
研究分析了 MF 模型的兩個常用訓練目標:
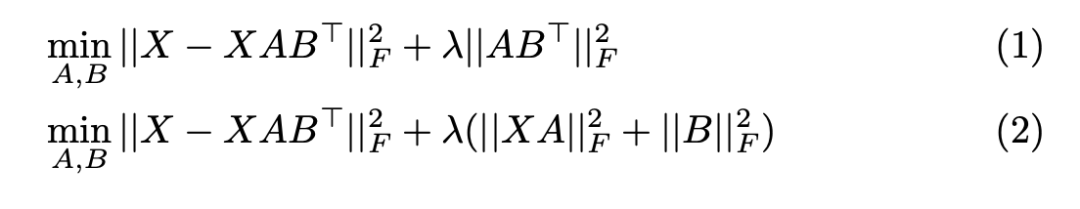
其中 X 是輸入數據矩陣,A 和 B 是學習到的嵌入矩陣,λ 是正則化參數。
問題根源:正則化與自由度
研究人員發現,第一個優化目標(等同於使用去噪或 dropout 的學習方式)在學習到的嵌入中引入了一個關鍵的自由度。這種自由度允許對嵌入維度進行任意縮放,卻不會影響模型的預測結果。
從數學角度來看,如果 Â 和 B̂ 是第一個目標的解,那麼對於任意對角矩陣 D,ÂD 和 B̂D^(-1) 也是解。這種縮放會影響學習到的嵌入的歸一化,從而影響它們之間的餘弦相似度。

來自論文:《Is Cosine-Similarity of Embeddings Really About Similarity? 》
舉兩個隨意產生結果的例子:
1. 在全秩 MF 模型中,通過適當選擇 D,item-item 餘弦相似度可以等於單位矩陣。這個奇怪的結果表明每個 item 只與自己相似,而與所有其他 item 完全不相似。
2. 通過選擇不同的 D,user-user 餘弦相似度可以簡化為 ΩA・X・X^T・ΩA,其中 X 是原始數據矩陣。這意味著相似度僅基於原始數據,完全沒有利用到學習的嵌入。
線性模型之外
除了線性模型,類似的問題在更複雜的場景中也存在:
1. 深度學習模型通常會同時使用多種不同的正則化技術,這可能會對最終嵌入的餘弦相似度產生意想不到的影響。
2. 在通過點積優化來學習嵌入時,如果直接使用餘弦相似度,可能會得到難以解釋且沒有實際意義的結果。
研究人員提出了幾種解決這些問題的方法:
-
直接針對餘弦相似度訓練模型,可能需要借助層歸一化等技術。
-
完全避免在嵌入空間中工作。相反,在應用餘弦相似度之前,先將嵌入投影回原始空間。
-
在學習過程中或之前應用歸一化或減少流行度偏差,而不是像餘弦相似度那樣僅在學習後進行歸一化。
語義分析中餘弦相似度的替代方案
在論文的基礎上,博客作者 Amarpreet Kaur 歸納了一些可以替換餘弦相似度的備選項:
-
歐幾里得距離:雖然由於對向量大小敏感而在文本數據中不太流行,但在嵌入經過適當歸一化時可以發揮作用。
-
點積:在某些應用中,嵌入向量之間的非歸一化點積被發現優於餘弦相似度,特別是在密集段落檢索和問答任務中。
-
軟餘弦相似度:這種方法除了考慮向量表示外,還考慮了單個詞之間的相似度,可能提供更細緻的比較。
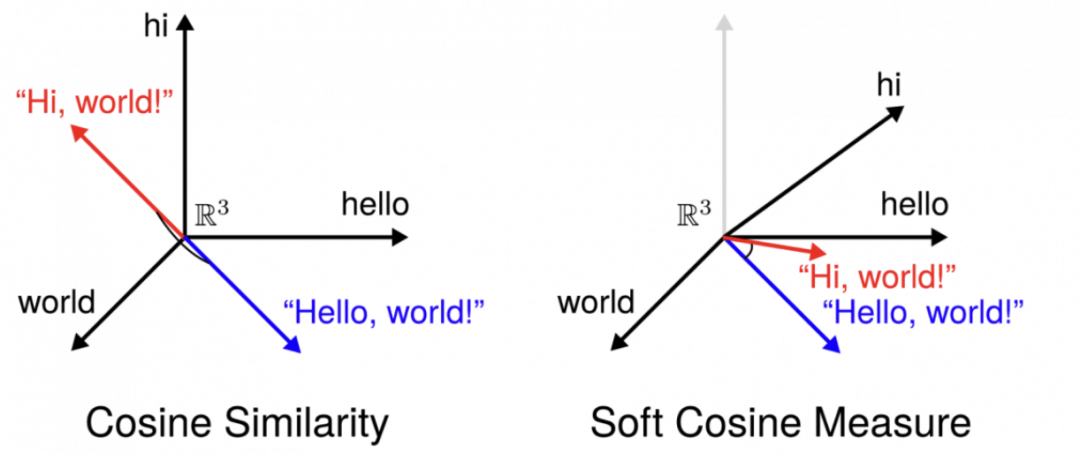
圖源:https://www.machinelearningplus.com/nlp/cosine-similarity/
-
語義文本相似度(STS)預測:專門為語義相似度任務訓練的微調模型 (如 STSScore) 有望提供更穩健和和更可解釋的相似度度量。
-
歸一化嵌入與餘弦相似度:在使用餘弦相似度之前,應用層歸一化等歸一化技術能有效提升相似度計算的準確性。
在選擇替代方案時,必須考慮任務的具體要求、數據的性質以及所使用的模型架構。通常需要在特定領域的數據集上進行實證評估,以確定最適合特定應用的相似度。
我們經常用「餘弦相似度」來計算用戶或物品之間的相似程度。這就像是測量兩個向量之間的夾角,夾角越小,相似度越高。論文中的實驗結果也表明,餘弦相似度給出的答案經常與實際情況不符。
在比較簡單的線性模型上都已經如此隨機,在更複雜的深度學習模型中,這個問題可能會更嚴重。因為深度學習模型通常使用更多複雜的數學技巧來優化結果,這些技巧會影響模型內部的數值大小,從而影響餘弦相似度的計算。
這就像是把一個本來就不太準的測量工具放在一個更複雜的環境中使用,結果可能會更不可靠。因此,需要尋找更好的方法,比如使用其他相似度計算方式,或者研究正則化技術對語義的影響。這提醒大家:在開發 AI 系統時,要多思考、多測試,確保工具真的好用。
對於這項研究的結論,你怎麼看?