300年後牛頓法得到改進，修改泰萊展開式，收斂速度更快

選自量子雜誌

作者：Kevin Hartnett

機器之心編譯

幾乎每一天，研究人員都在尋找最優解。他們可能需要確定大型航空樞紐的最佳選址，或者如何在投資組合中最大化收益的同時最小化風險，又或者開發能夠區分交通燈和停車標誌的自動駕駛汽車。

從數學角度來看，這些問題都可轉化為對函數最小值的搜索。

但在所有這些場景中，函數都過於複雜，無法直接評估。研究人員不得不採用近似方法求取極值。

事實證明，最有效的方法之一源自艾沙克・牛頓 300 多年前提出的牛頓法。這個算法相當簡單，有點像蒙著眼睛在陌生的場景中尋找最低點。當你把一隻腳放在另一隻腳前面時，你需要的唯一信息就是你是在上坡還是下坡，坡度是在上升還是在下降。利用這些信息，你可以相對較快地得到近似最小值。

在 17 世紀 80 年代，艾沙克・牛頓發明了一種尋找最優解的算法。三個世紀後，數學家們仍在使用和完善他的方法。

至今，該算法仍展現出驚人的威力 —— 從物流金融到計算機視覺乃至純數學領域，是解決現代問題的關鍵工具。

但牛頓法也存在顯著缺陷：並非適用於所有函數。為此，數學家們持續優化該技術，在保持計算效率的同時不斷拓展其應用邊界。

去年夏天，三位研究人員對牛頓法進行了改進，他們分別是來自普林斯頓大學的教授 Amir Ali Ahmadi，佐治亞理工學院博士後研究員 Abraar Chaudhry（曾經是 Amir Ali Ahmadi 的學生），以及耶魯大學博士後研究員 Jeffrey Zhang，這三人將牛頓法擴展到迄今為止最廣泛的函數類別，使其能夠高效運行。

• 論文地址：https://arxiv.org/pdf/2311.06374

• 論文標題：Higher-Order Newton Methods with Polynomial Work per Iteration

尋找最小值

通常，數學中的函數是將輸入值轉化為輸出值，函數最關鍵的特徵之一是其最小值。

但找到最小值的過程充滿挑戰，例如函數可能包含數十個高次冪變量，使公式化分析難以實現。

早在 17 世紀 80 年代，牛頓就發現：即便面對極其複雜的函數，我們始終能獲取兩類關鍵信息來定位最小值。首先是函數的一階導數（即斜率），反映特定點位的函數變化陡峭程度；其次是斜率自身的變化率（二階導數），揭示函數曲率的變化特徵。

Amir Ali Ahmadi 

假設你要尋找某個複雜函數的最小值。首先，選擇函數上一個你認為可能接近真實最小值的點。計算該點處函數的一階導數和二階導數。這些導數可以用來構建一個特殊的二次方程 —— 如果函數處於二維平面中，這是一個拋物線；如果函數是更高維度的，這是一個類似杯子形狀的拋物面，這個二次方程被稱為泰萊近似。

現在，計算這個二次方程的最小值，而不是原來的複雜函數 —— 這是很容易做到的。然後，將這個點的坐標重新代入原來的函數，你會得到函數上的一個新點，這個新點應該更接近函數的真實最小值。

牛頓證明了，如果你不斷地重覆這個過程，你最終會逐步逼近原來那個更複雜函數的最小值。不過，這種方法並不總是奏效，尤其是當你從一個距離真實最小值太遠的點開始時。但大部分情況下，它是有效的，並且它有一些非常理想的特性。

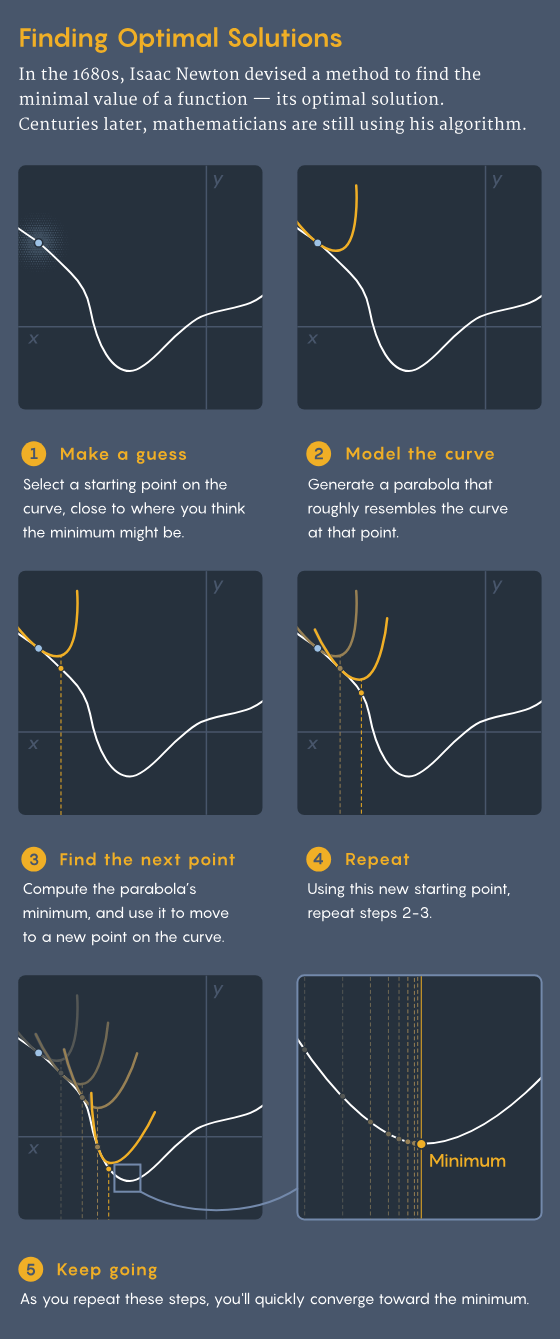
諸如其他迭代方法，如梯度下降法（當今機器學習模型中使用的算法），以線性速率收斂到真實最小值。牛頓法以「二次」速率收斂到真實最小值的速度要快得多，因為它可以比梯度下降法用更少的迭代次數確定最小值。

然而，牛頓法的每次迭代比梯度下降法的迭代更耗費計算資源，這就是為什麼研究人員在某些應用（如訓練神經網絡）中更喜歡使用梯度下降法。但牛頓法仍然非常高效，在各種情況下都很有用。

時光回溯，如果牛頓不僅僅滿足於一階和二階導數，而是取三階和四階導數，他或許可以更快地編寫收斂到真實最小值的方法。這將使他得到更複雜的泰萊高階近似。

這種高階泰萊近似，雖然超越了牛頓時代的數學框架，但其核心思想 —— 將複雜函數簡化為更易處理的模型 —— 至今仍啟發著現代優化理論的發展。

Ahmadi 曾說：「牛頓在二次多項式中做到了這一點。他這樣做是因為沒有人知道如何最小化高階多項式」。

在此後的幾個世紀里，數學家們一直致力於擴展他的方法，探索他們能從更複雜的函數泰萊近似中榨出多少信息。

例如，在 19 世紀，俄羅斯數學家帕夫努蒂・切比雪夫提出了牛頓法的一個版本，用三次方程（指數為 3）來近似函數。但當原始函數涉及多個變量時，他的算法不起作用。

在 2021 年，尤里・涅斯捷羅夫（Yurii Nesterov 現就職於布達佩斯考文紐斯大學）展示了如何用三次方程有效地近似任意數量變量的函數。儘管如此，他的方法在嘗試使用四次方程、五次方程等更高階近似時，卻無法保持其效率。這一證明無疑成為了該領域的一大突破。

如今，Ahmadi、Chaudhry 和 Zhang 將尤里・涅斯捷羅夫的結果又推進了一步。他們的算法不僅適用於任意數量的變量，還能處理任意階數的導數。此外，他們的算法在所有這些情況下都保持了高效性 —— 這在之前是無法想像的。

但首先，他們必須找到一種方法來讓一個困難的數學問題變得容易得多。

Jeffrey Zhang

尋找優化空間

在數學優化的世界中，對於高次冪函數的最小值求解，目前尚無快速通用的方法 —— 這一直是牛頓法的主要局限。不過，某些特定類型的函數因其特性而易於優化。

在最新的研究中，Ahmadi、Chaudhry 和 Zhang 的研究團隊證明了一個重要的發現：證明總是可以找到具有這些特徵的近似方程。然後他們展示了如何調整這些方程以有效地運行牛頓法。

那什麼樣的性質使得一個方程易於最小化呢？關鍵在於兩點：

• 第一，方程應該是碗狀的，或「凸的」。它只有一個穀值，而不是許多穀值 —— 這意味著當你試圖最小化它時，無需擔心會將任意一個低谷誤認為是最低點。

• 第二個性質是方程可以寫成平方和。例如，

  ，可以寫成

  

  之和。

近年來，數學家已開發出針對任意高次冪函數的優化技術 —— 只要函數同時滿足凸性和平方和特性。

Abraar Chaudhry 和兩位同事最近發現了一種改進數百年來尋找函數最小值的方法。

但這些技術始終無法與牛頓法有效兼容，因為泰萊近似在大多數情況下並不具備這些優良特性。

但 Ahmadi、Chaudhry 和 Zhang 通過引入一種稱為半正定規劃（semidefinite programming）的技術來對泰萊近似進行足夠的調整，使其既是平方和又是凸函數，同時調整幅度不脫離它相似的原始函數。

他們本質上在泰萊展開式中添加了一個修正因子，將其變成了一個具有兩個所需屬性的方程。

Ahmadi 提到「我們可以稍微改變泰萊展開式，使其更容易最小化。想像一下泰萊展開式，但經過一些調整。」

他和他的同事隨後表明，使用這個修改後的泰萊展開式版本（涉及任意多個導數），他們的算法仍然能夠收斂到原始函數的真實最小值。更重要的是，收斂速度會隨著所用導數的數量而提升：正如使用二階導數使牛頓法以二次速率接近最小值，使用三階導數則使研究者們能夠以三次速率接近，依此類推。

通過這一創新，Ahmadi、Chaudhry 和 Zhang 成功創建了一個更強大的牛頓法版本，與以前的技術相比，它可以用更少的迭代次數達到函數的真實最小值。

與牛頓法的原始版本一樣，這種新算法的每次迭代在計算上仍然比梯度下降等方法更昂貴。因此，目前這項新工作不會改變自動駕駛汽車、機器學習算法或空中交通管製系統的工作方式。在這些情況下，最好的選擇仍然是梯度下降。

賓夕法尼亞大學的 Jason Altschuler 說：「優化中的許多想法需要數年時間才能完全實用。但這似乎是一個全新的視角。」

然而，隨著時間的推移，如果運行牛頓法所需的基礎計算技術變得更加高效 —— 即每次迭代的計算成本降低 —— 那麼 Ahmadi、Chaudhry 和 Zhang 開發的算法最終可能會在包括機器學習在內的各種應用中超越梯度下降。

Ahmadi 表示「從理論上講，我們目前的算法是更快的」，而後他進一步補充道，希望在未來 10 到 20 年內，在實踐中能同樣如此。

這一研究為牛頓法注入了新的活力，儘管目前尚未達到完全實用的階段，但其潛力不容忽視。在計算技術不斷進步的背景下，這一算法有望在未來成為優化領域的核心工具之一。

原文鏈接：https://www.quantamagazine.org/three-hundred-years-later-a-tool-from-isaac-newton-gets-an-update-20250324/