更長思維並不等於更強推理性能，強化學習可以很簡潔

機器之心報導

編輯：Panda

今天早些時候，著名研究者和技術作家 Sebastian Raschka 發佈了一條推文，解讀了一篇來自 Wand AI 的強化學習研究，其中分析了推理模型生成較長響應的原因。

他寫到：「眾所周知，推理模型通常會生成較長的響應，這會增加計算成本。現在，這篇新論文表明，這種行為源於強化學習的訓練過程，而並非更高的準確度實際需要更長的答案。當模型獲得負獎勵時，強化學習損失函數就傾向於生成較長的響應，我認為這能解釋純強化學習訓練為什麼會導致出現頓悟時刻和更長思維鏈。」

也就是說，如果模型獲得負獎勵（即答案是錯的），PPO 背後的數學原理會導致響應變長，這樣平均每個 token 的損失就更小一些。因此，模型會間接地收到鼓勵，從而使其響應更長。即使這些額外的 token 對解決問題沒有實際幫助，也會出現這種情況。

響應長度與損失有什麼關係呢？當使用負獎勵時，更長的響應可以稀釋每個 token 的懲罰，從而讓損失值更低（即更好 —— 即使模型仍然會得出錯誤的答案。

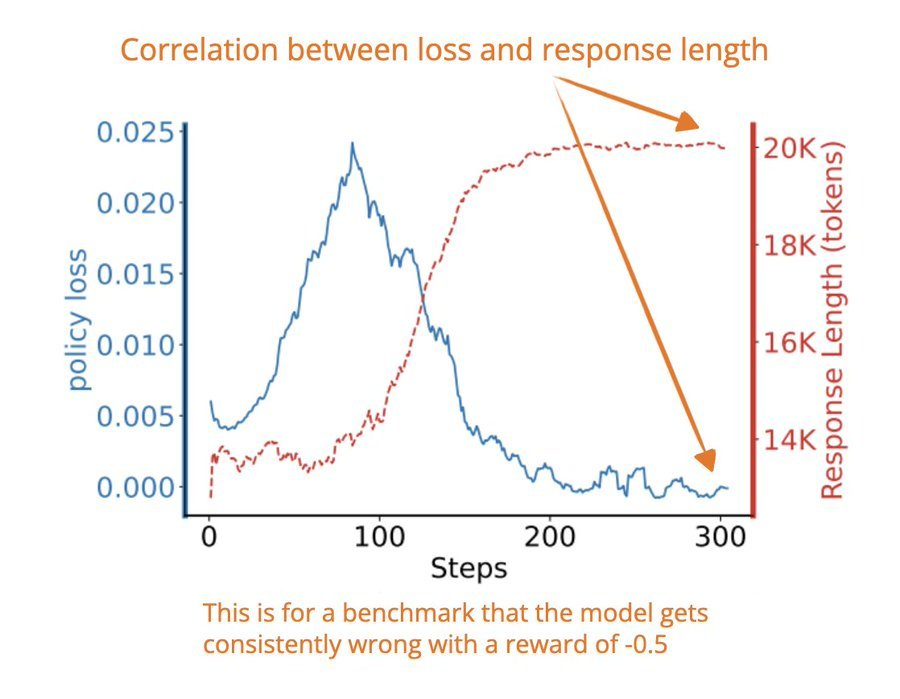
因此，模型會「學習」到：即使較長的回答對正確性沒有幫助，也能減少懲罰。

此外，研究人員還表明，第二輪強化學習（僅使用一些有時可解的問題）可以縮短回答時間，同時保持甚至提高準確度。這對部署效率具有重大意義。

以下是該論文得到的三大關鍵發現：

• 簡潔性與準確度之間的相關性：該團隊證明，在推理和非推理模型的推斷（inference）過程中，簡潔的推理往往與更高的準確度密切相關。

• 對 PPO 損失函數的動態分析：該團隊通過數學分析，建立了響應正確性與 PPO 損失函數之間的聯繫。具體而言，研究表明，錯誤的答案往往會導致響應較長，而正確的答案則傾向於簡潔。

• 有限的數據：該團隊通過實驗證明，即使在非常小的數據集上，強化學習的後訓練階段仍然有效，這一結果與文獻中的當前趨勢相悖，並且強化學習後訓練在資源受限的場景下也是可行的。

有研究者認為這項研究揭示了強化學習存在的一個普遍問題：訓練的目標只是為了獲得獎勵，而並非是解決問題。

下面我們就來具體看看這篇論文。

• 論文標題：Concise Reasoning via Reinforcement Learning 

• 論文地址：https://arxiv.org/abs/2504.05185

響應更長≠性能更好

下表展示了使用不同模型在不同基準測試上，答案正確或錯誤時的平均響應長度。藍色小字表示用於計算所得平均值的樣本數。

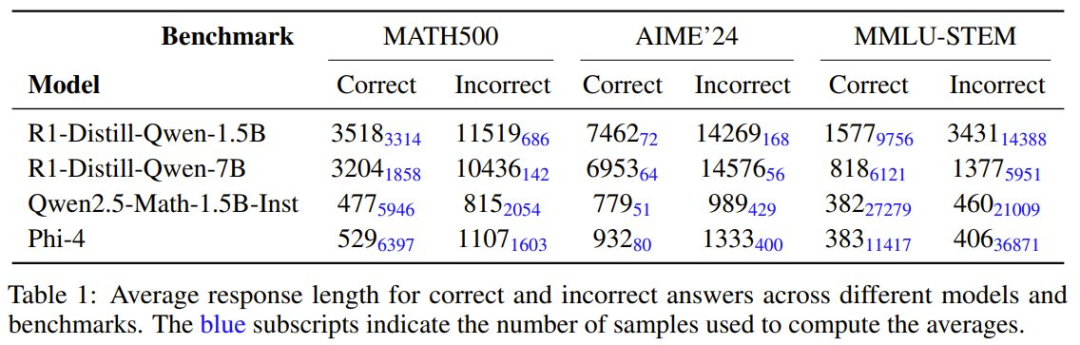
由此可知，更長響應不一定能帶來更好的性能。

於是問題來了：使用 RL 訓練的 LLM 傾向於在什麼時候增加響應長度？原因又是為何？

每個推理問題都是一個 MDP

從根本上講，每個推理問題（例如，數學問題）都構成了一個馬爾可夫決策過程 （MDP），而不僅僅是一個靜態樣本。

MDP 由狀態空間 S、動作空間 A、轉換函數 T、獎勵函數 R、初始狀態分佈 P_0 和折扣因子 γ 組成。

在語言建模中，每個 token 位置 k 處的狀態由直到 k 為止并包括 k 的所有 token（或其嵌入）組成，另外還包括上下文信息（例如問題陳述）。動作空間對應於可能 token 的詞彙表。轉換函數可確定性地將新的 token 附加到序列中。除了最後一步之外，所有步驟的獎勵函數都為零。在最後一步，正確性根據最終答案和格式進行評估。初始狀態取決於提示詞，其中可能包含問題陳述和指令（例如，「逐步求解並將最終答案放入方框中」）。強化學習的目標是最大化預期回報，預期回報定義為根據 γ 折扣後的未來獎勵之和。在 LLM 的後訓練中，通常將 γ 設置為 1。

為了在僅提供最終答案的情況下解決問題，需要一個能夠偶爾得出正確答案的基礎模型。在對多個問題進行訓練時，整體 MDP 由多個初始狀態和更新的獎勵函數組成。添加更多問題會修改 P_0 和 R，但會保留基本的 MDP 結構。

這會引入兩個重要的考慮因素：(1) 更大的問題集會增加 MDP 的複雜性，但這可能會使所學技術具有更高的泛化能力。(2) 原理上看，即使是單個問題（或一小組問題）也足以使強化學習訓練生效，儘管這可能會引發過擬合的問題。

過擬合是監督學習中的一個問題，因為模型會記住具體的例子，而不是進行泛化。相比之下，在線強化學習則不會受到這個問題的影響。與依賴靜態訓練數據的監督學習不同，在線強化學習會持續生成新的響應軌跡，從而使模型能夠動態地改進其推理能力。此外，在線強化學習不僅僅是模仿預先定義的解答；它還會主動探索各種推理策略，並強化那些能夠得出正確答案的策略。

兩種關鍵機制促成了這種穩健性：(1) 采樣技術（例如非零溫度）可確保生成的響應具有變化性；(2) 訓練期間持續的模型更新會隨著時間的推移引入新的響應分佈，從而防止訓練停滯和過擬合。

這能解釋在小規模問題集上進行強化學習訓練會保持有效性的原因。該團隊表示，之前還沒有人報告過將強化學習訓練應用於極小數據集的研究，這也是本研究的貢獻之一。

除了數據大小的考慮之外，需要強調的是，強化學習的唯一目標是最小化損失，這也就相當於最大化預期回報。從這個角度來看，強化學習訓練過程中響應長度的任何顯著變化都必然是由損失最小化驅動的，而非模型進行更廣泛推理的固有傾向。

為了進一步研究這一點，該團隊基於 DeepSeek-R1-Distill-Qwen-1.5B 基礎模型，使用近端策略優化 (PPO) 算法進行了強化學習訓練。訓練數據是從 OlympiadBench 數據集中選擇的四個問題。

之所以特意選擇這些問題，是因為即使進行了廣泛的采樣，基礎模型也始終無法解決這些問題，導致終端獎勵恒定為 -0.5。其上下文大小限制為 20K token，該團隊繪製了策略損失與響應長度的關係圖（參見圖 1）。

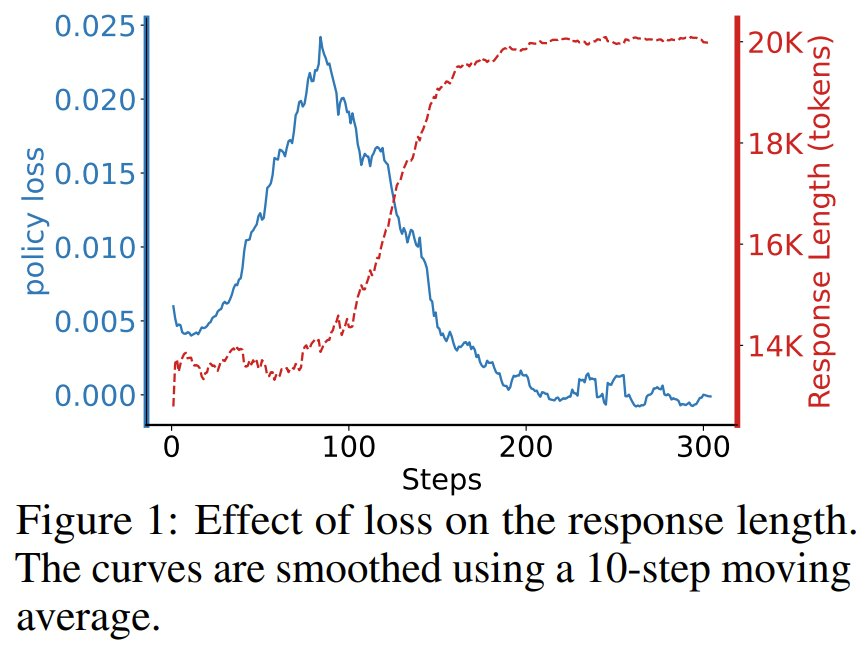
結果清楚地表明，響應長度和損失之間存在很強的相關性：隨著響應長度的增加，損失持續下降。這直接證明：損失最小化（而非模型產生更長響應的內在趨勢）才是驅動響應長度增長的主要動力。

對於 PPO 對響應長度的影響，該團隊也從數學角度進行瞭解釋。詳見原論文。

一種兩階段強化學習策略

該團隊的分析突出了幾個要點。

• 當在極其困難的問題訓練時，響應長度往往會增加，因為較長的響應更有可能受到 PPO 的青睞，因為模型難以獲得正回報。

• 當在偶爾可解的問題上訓練時，響應長度預計會縮短。

• 在大規模訓練場景中，響應長度的動態會變得非常複雜，並會受到底層問題難度的巨大影響。

該團隊認為，由於大多數問題至少偶爾可解，因此平均響應長度最終會減少。值得注意的是，該團隊目前的分析不適用於 GRPO，對此類方法的精確分析還留待未來研究。儘管如此，由於簡潔性與更高準確度之間的相關性，該團隊推測：如果訓練持續足夠長的時間，這種增長最終可能會停止並開始逆轉。

如果數據集包含過多無法解決的問題，那麼從「鼓勵響應更長」到「鼓勵簡潔性」的轉變可能會大幅延遲且成本高昂。

為瞭解決這個問題，該團隊提出了一種新方法：通過一個後續強化學習訓練階段來強製實現簡潔性，該階段使用了偶爾可解問題的數據集。於是，就能得到一種兩階段的強化學習訓練方法：

在第一階段，用高難度問題訓練模型。此階段的目標是增強模型解決問題的能力，由於 PPO 主要會遇到負獎勵，從而促使模型產生更長的響應，因此響應長度預計會增加。值得注意的是，第一階段也可被視為現有推理模型的強化學習訓練。

在第二階段，使用非零 p_a（偶爾可解）的問題繼續訓練。此階段能在保持甚至提高準確度的同時提升簡潔性。值得注意的是，正如後面將看到的，它還能顯著提高模型對降低溫度值的穩健性 —— 即使在有限的采樣量下也能確保卓越的性能。

從 MDP 的角度，該團隊得到了一個關鍵洞察：即使問題集很小，也可以實現有效的強化學習訓練，儘管這可能會降低泛化能力。尤其要指出，在訓練的第二階段 —— 此時模型已經具備泛化能力，即使僅有只包含少量問題的極小數據集也可使用 PPO。

實驗結果

該團隊也通過實驗檢驗了新提出的兩階段強化學習訓練方法。

問題難度如何影響準確度-響應長度的相關性

圖 2 給出了準確度和響應長度隨訓練步數的變化。

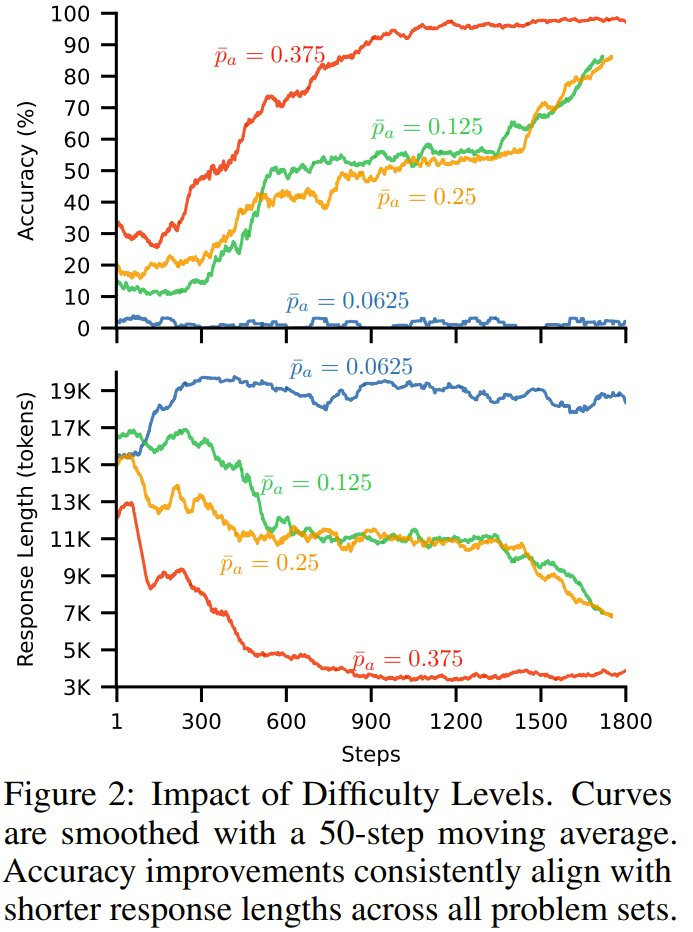
可以看到，在所有問題集中，準確度的提高與響應長度的縮短相一致 —— 這表明隨著模型準確度的提高，其響應長度也隨之縮短。此外，對於更簡單的問題集，響應長度縮短得更快。最後，對於最難的數據集，由於問題很少能夠解決，因此響應長度有所增加。

響應長度減少

圖 3 展示了在不同的測試數據集（AIME 2024、AMC 2023 和 MATH-500）上，經過後訓練的 1.5B 和 7B 模型的準確度和響應長度隨訓練步數的變化情況。

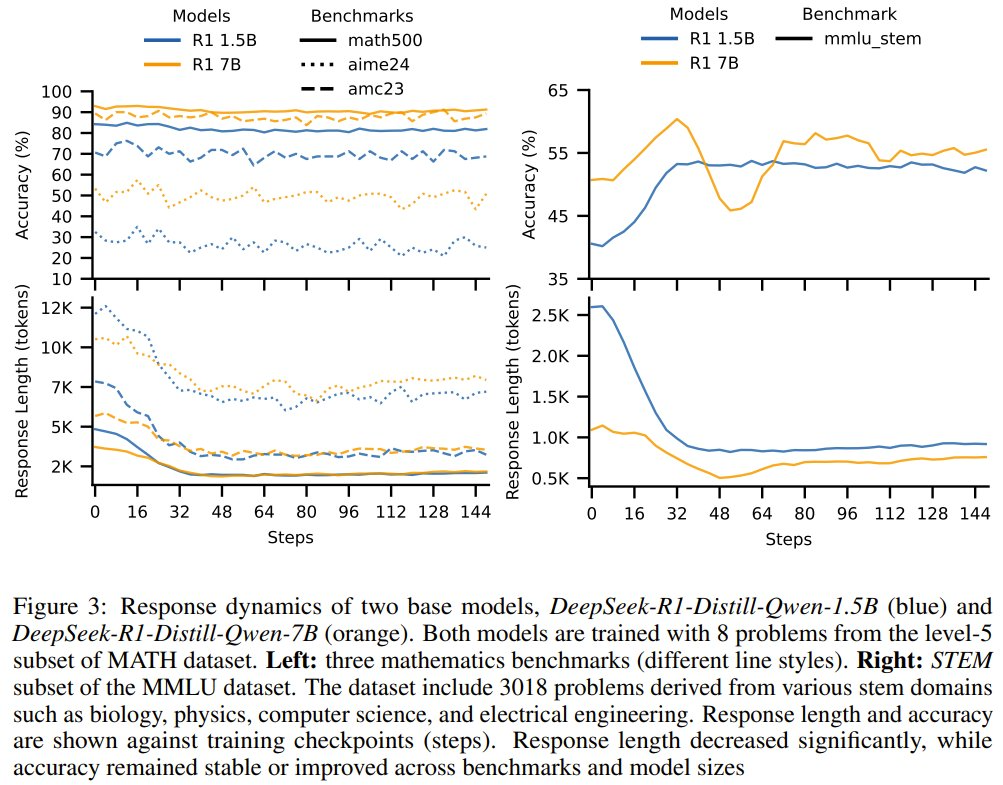
可以看到，新提出的兩階段強化學習訓練方法會讓響應長度顯著下降，同時準確度會保持穩定。而右圖在 MMLU_STEM 上的結果更是表明：僅使用 8 個樣本，強化學習後訓練也能帶來準確度提升。

性能和穩健性的提升

前面的實驗結果已經證明：進一步的強化學習後訓練可以在保持準確度的同時縮短響應長度。該團隊進一步研究發現：進一步的強化學習後訓練也能提升模型的穩健性和性能。

為了評估模型的穩健性，該團隊檢查了它們對溫度設置的敏感性。將溫度設置為零會大幅降低 R1 等推理模型的準確度。然而，諸如 pass@1 之類的標準指標依賴於非零溫度下的多個樣本，這通常會掩蓋在小型數據集上進行二次強化學習後訓練的優勢。

該團隊使用 0 和 0.6 的溫度值進行了實驗，結果見表 3。

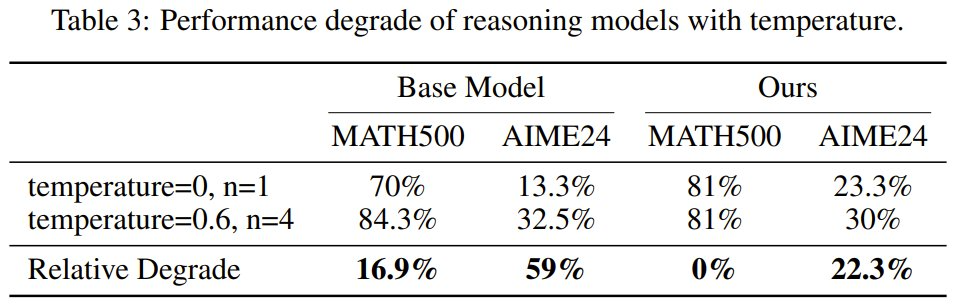
可以看到，當溫度設置為 0 時，經過後訓練的模型的表現顯著優於基線模型，這表明經過後訓練的模型與基線模型相比更加穩健。

該團隊還表明，在有限數量的樣本上進行進一步的強化學習訓練可以顯著提升準確度。這種效果取決於先前在類似（甚至相同）問題上進行過的強化學習訓練程度。如果模型已經進行過大量強化學習訓練，可能就更難以進一步提升準確度。

為了探究這一點，該團隊基於 Qwen-Math-v2.5 使用了在線強化學習進行實驗，訓練樣本是來自 MATH 數據集的 4 個樣本。不同於 R1，該模型之前並沒有經過強化學習訓練，而是僅在大量數學數據上進行了 token completion 訓練。結果見表 4。

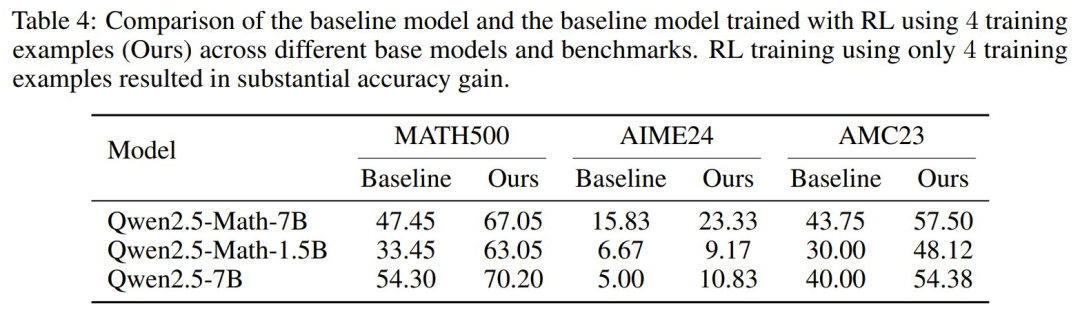
可以看到，提升很驚人！在 1.5B 模型上，提升高達 30%。這表明，就算僅使用 4 個問題進行強化學習後訓練，也能得到顯著的準確度提升，尤其是當模型之前未進行過強化學習推理優化訓練時。

參考鏈接

https://x.com/rasbt/status/1911494805101986135