50s完成7B模型量化,4bit達到新SOTA,大模型低比特量化有新招了 | NeurIPS 2024 Oral
DuQuant團隊 投稿量子位 | 公眾號 QbitAI
消除激活值(outliers),大語言模型低比特量化有新招了——
自動化所、清華、港城大團隊最近有一篇論文入選了NeurIPS 2024(Oral Presentation),他們針對LLM權重激活量化提出了兩種正交變換,有效降低了outliers現象,達到了4-bit的新SOTA。

簡單理解,在大語言模型(LLM)中,有一些中間層輸出的數值(激活值 Activation)會變得非常大,它們被稱為「outliers(離群值)」,這些 outliers給模型量化帶來了挑戰。
補充一下,量化可以將模型中的數值從浮點數轉換為整數,以減少模型的大小和計算需求。
而一旦在量化過程中存在大量outliers,會導致量化後的模型性能下降。
明白了這層道理, 我們再來看他們團隊的一項名為DuQuant的新研究。
首先, 他們發現在LLM的前饋網絡 (FFN) 模塊中的down_proj層, 存在明顯的Massive Outliers(非常大的激活值)。
這種outliers不同於以往發現的Normal Outliers,表現為大於絕對值幾百的異常值並局限於個別的tokens中——
它們導致現有的量化算法(如SmoothQuant和OmniQuant)在將模型的權重和激活值量化為4位二進製數時表現不佳。
對此,團隊提出了一種新的量化方法,叫做DuQuant。
DuQuant通過學習旋轉和置換變換矩陣,在Activation矩陣內部將outliers轉移到其他通道,最終得到平滑的激活矩陣,從而大幅降低了量化難度。
實驗顯示,使用DuQuant方法,在4位權重和激活量化的設置下,模型達到了SOTA。
同時,DuQuant的訓練非常快速,可以在50s內完成7B模型的量化過程,即插即用。

背景
在每個Transformer塊的常見模塊中,多頭自注意力(MSA)和前饋網絡(FFN)基本上都由線性層組成,將其表示為:
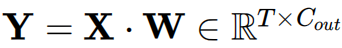
其中


表示權重矩陣。
是激活輸入,
模型量化通過將浮點數(FP16, BF16)表示的模型權重或激活值轉換為低位的浮點數或整數來減少內存佔用,權重激活量化可以通過使用低比特乘法的算子進一步加快模型推理的速度。
該工作重點關注低比特整型量化,目標是獲得更好的硬件支持。
具體來說, 𝖻位量化過程將FP16張量𝐗映射為低位整數𝐗𝗊 :

符號⎣ · ⎤表示最接近的舍入操作, ∆是量化步長, 𝑧表示零點。
遵循主流量化方法,作者對激活𝐗採用逐token量化,對權重𝐖採用逐通道量化,這意味著為𝐗的每個token分配不同的步長( ∆𝐗 ∊ ℝ𝑻x1),為𝐖的每個輸出通道分配不同的步長
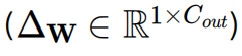
動機(Motivation)
據作者介紹,他們首次在實驗中發現,LLM FFN模塊中的down_proj layer存在明顯的Massive Outliers(非常大的激活值),表現為絕對值大於幾百的異常值並局限於個別的token中。
PS:先前工作發現Massive Outliers存在於每個transformer block的輸出中,DuQuant的作者進一步將其定位在FFN模塊中。

論文:https://link.zhihu.com/?target=https%3A//eric-mingjie.github.io/massive-activations/index.html
這些Massive Outliers造成SmoothQuant和OmniQuant等算法在4bit WA量化中表現較差。
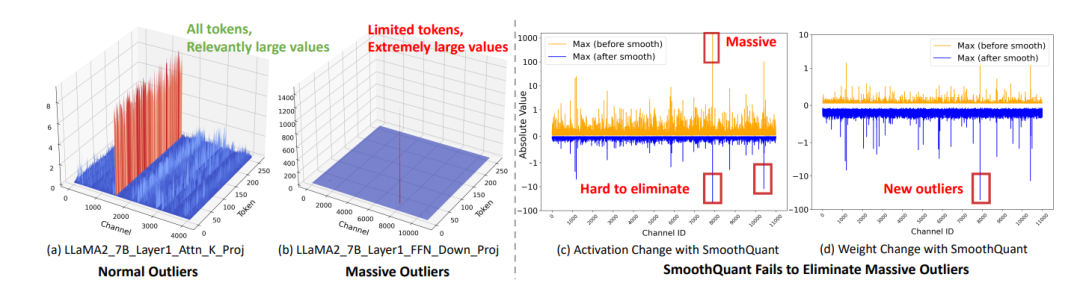 △圖1:Massive outliers顯著加大了低比特權重激活量化的難度
△圖1:Massive outliers顯著加大了低比特權重激活量化的難度圖1(a)(b)對比了普遍常見的Normal Outliers,和在FFN中出現的Massive Outliers。
SmoothQuant通過將激活值除以每通道平滑因子並將其乘回權重矩陣,嘗試將量化難度從激活值轉移到權重。
具體來說,SmoothQuant使用逐通道的平滑對角矩陣,記為𝞚 ,將原始線性層重新表達為:𝐘=𝐗 · 𝐖=(𝐗 ·𝞚)(𝞚-1 · 𝐖),對角矩陣𝞚中的元素𝞚𝑗 的計算方式為:

其中α是一個超參數,表示遷移強度。
然而,作者觀察到在輸入端進行這種轉移可能會導致權重矩陣也出現明顯的難以量化的outliers(如圖1(d)所示),這一問題的根源在於Massive Outliers使平滑因子𝞚𝑗 變得異常大。
此外,極大的outliers還可能導致基於優化的方法出現梯度爆炸的問題,所以基於梯度優化的OmniQuant和AffineQuant等工作會直接跳過down_proj layer,直接退化為SmoothQuant的處理方式。
這些preliminary experiments都表明需要一種更新更好的方式處理兩種outliers,特別是平滑掉down_proj輸入側的Massive Outliers。
方法
DuQuant提出通過學習旋轉和置換變換矩陣,在Activation矩陣內部將outliers轉移到其他通道,最終得到平滑的激活矩陣,從而大幅度降低了量化難度。
(a) 逐步展示了DuQuant算法對Normal outlier的處理過程,(b) DuQuant顯著降低了Massive outlier,(c)一個Tony Example說明DuQuant有效降低了激活矩陣的量化難度。
 △圖2:DuQuant算法說明
△圖2:DuQuant算法說明簡單來說,DuQuant算法包含三個步驟:
1)旋轉矩陣的構造有效利用了特定outlier channel的位置索引,作者使用了分塊對角的旋轉矩陣,在每個block內部通過貪心算法將outlier平攤到其他的channels中。
2)由於block size的限制,可能導致某些block在旋轉之後組內的平均值大於其他blocks,因此作者進一步使用通道置換技術重新分配activation channel,使用zigzag順序排列使各組均值的方差大幅減小。
3) 進一步執行一次旋轉變換達到更均勻的activation分佈,從而大幅降低了量化難度。
旋轉矩陣:作者希望應用旋轉矩陣𝐑進行行或列變換,減輕Normal Outliers和Massive Outliers的影響。
由於Massive Outliers通常隨機分佈在激活空間中,直接找到能夠通過單次旋轉變換減輕outliers的最優旋轉矩陣𝐑是具有挑戰性的。
為瞭解決這一問題,作者採用帶有先驗知識的貪心搜索方法來計算旋轉矩陣
,從而近似理想的旋轉矩陣𝐑。
具體來說,
的計算包括以下步驟:
1、識別outliers主要集中的特徵維度 ,即:

,其中, 𝐗𝑖𝑗表示𝐗中第𝑖行和第𝑗列的元素。
2、基於搜索到的維度,構建旋轉矩陣如下:

是用於交換激活值的第1列和第d(1) 列的交換矩陣,表示一個正交初始化的旋轉矩陣,其第一行均勻分佈。
這樣做的目的是通過
變換後減輕第1列中的outliers。
為了進一步增加隨機性,保留減輕outliers後的第1列,並通過與隨機正交矩陣𝐐’相乘,隨機旋轉其他列。
3、設N為貪心搜索的步數,則近似的旋轉矩陣

,其中

。每個𝐑𝑖 根據公式(2)和識別到的特徵維度d(𝑖) 構建。
通過這種構建方式,可以確保近似的最優旋轉矩陣能夠有效減輕具有較大幅度的outliers,而不僅僅是使用隨機選擇的正交旋轉矩陣。
然而,直接構建整個旋轉矩陣非常耗時,並且會導致大量的內存開銷。
為了實現快速矩陣乘法,參考Training Transformer with 4ibts ,作者選擇以分塊的方式近似旋轉矩陣


其中,

表示第𝑖個塊的方陣,該矩陣按照上述三步構建。塊的數量K通過K=C𝑖n/2n計算得出。
通道置換矩陣:儘管採用了塊對角旋轉矩陣
來提高時間和存儲效率,但其專注於局部信息的特性帶來了進一步減少outliers的潛在限制。
由於在每個小塊內進行的旋轉變換無法整合跨不同塊的信息,一個塊中可能有相對較大的outliers,而另一個塊中則有較小的outliers,導致不同塊之間存在較高的方差。
因此,作者提出利用通道置換矩陣平衡不同blocks之間outliers的幅度。
具體來說,在每個小塊中,將維度d𝑗中最大的outlier記為O𝑗。
同時, Mb𝑖表示第𝑖個塊中所有O𝑗的平均值,其中𝑖=1,2,……,K ,各個塊之間激活幅度的方差可以表示為:

作者引入了之字形置換矩陣P 。
具體來說,通過生成一個之字形序列,首先將激活值最高的通道分配給第一個塊,接著,將激活值次高的通道按遞減順序分配到後續的塊,直到第K個塊。
在到達最後一個塊後,順序反轉,從下一個激活值最高的通道開始,按遞增順序分配。
這個往複模式貫穿所有塊,確保沒有單個塊持續接收最高或最低激活值的通道。
通過使用之字形置換,DuQuant實現了不同塊之間outliers的均衡分佈,從而能夠使用額外的旋轉變換進一步平滑outliers,如圖2所示。
需要注意的是:
1、通道置換其實是非常重要的一步,也很簡單快速(對於推理效率的影響很小,可見後面實驗部分),既可以避免像SpinQuant那樣複雜的訓練流程,也比QuaRot的Hadamard旋轉性能表現更好。
2、旋轉矩陣和置換變換矩陣都是正交矩陣,保證了𝐗𝐖輸出的不變性,作者還通過嚴謹的理論推導了證明了兩種變換有效降低了量化誤差,具體證明可以閱讀Paper裡面的Appendix。
實驗
在4-bit setting下達到了SOTA的效果,DuQuant驗證了LLaMA、Vicuna、Mistral系列模型,在PPL、QA、MMLU和MT-Bench等任務上都明顯提升了量化模型的性能。
此外作者還在LongBench評測了量化模型長文本生成的能力,DuQuant同樣大幅超過了baselines。
 △DuQuant在LLaMA3-8B的低比特量化中顯著超過了基線方法
△DuQuant在LLaMA3-8B的低比特量化中顯著超過了基線方法上面是DuQuant在LLaMA3模型的量化效果,更多的模型和task上的表現可以參見論文。
硬件測速也證明了DuQuant在pre-filing階段可以達到2.08倍的加速比,在decoding階段有效降低了3.50倍內存開銷。

同時如右圖所示,DuQuant相比INT4推理帶來額外的10%左右速度開銷,微高於QuaRot,但帶來更多性能提升。

此外,DuQuant與使用Hadamard旋轉矩陣的QuaRot主要有以下兩點不同:
1、DuQuant構造的旋轉矩陣利用了先驗知識(具體的outlier channel索引),因此它可以比QuaRot更好地平滑激活空間,如下圖展示了DuQuant單次旋轉和Hadamard旋轉對LLaMA2-7B Attention Key_proj輸入的變換效果。
2、QuaRot依賴於耗時的GPTQ算法來提升性能,而作者引入的通道置換矩陣可以幫助DuQuant在極短時間內進一步平衡outliers的分佈,兩種正交變換可以同時平滑權重矩陣的空間,降低權重矩陣的量化難度,從而取得更好效果。

小結一下,DuQuant通過兩種正交變換,利用activation激活值的先驗知識達到了比QuaRot中Hadamard旋轉更好的量化效果。
該工作獲得了審稿人一致的高度評價,並最終被選為Oral Presentation,錄取率0.4%。
更多細節歡迎查閱原論文。
項目主頁:
https://duquant.github.io/
論文:
https://arxiv.org/abs/2406.01721
代碼:
https://github.com/Hsu1023/DuQuant